单选题设某人群的身高X服从N(155.4,5.32)分布,现从该总体中随机抽出一个n=10的样本,得均值为X=158.36,S=3.83,求得μ的95%可信区间为(155.62,161.10),发现该区间竟然没有包括真正的总体均数155.4。若随机从该总体抽取含量n=10的样本200个,每次都求95%置信区间,那么类似上面的置信区间(即不包括155.4在内)大约有().A 5个B 20个C 10个D 1个E 190个
题目
5个
20个
10个
1个
190个
相似考题
更多“设某人群的身高X服从N(155.4,5.32)分布,现从该总体中随机抽出一个n=10的样本,得均值为X=158.36,S”相关问题
-
第1题:
从均数为μ的正态分布总体中随机取含量为n的样本,样本均数为。服从t分布的随机变量是
A.X-σ
B.X-σX
C.X-μσ
D.X-μσX
E.-μSX
正确答案:E
-
第2题:
(130~131题共用备选答案)
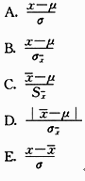
从正态分布总体X~N(μ,σ)中随机抽取含量为n的样本,样本均数为
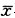 ,服从标准正态分布的随机变量是正确答案:A
,服从标准正态分布的随机变量是正确答案:A
(答案:A)根据卢变换定义。 -
第3题:
设X~N(μ,0.09)从中随机抽取样本量为4的样本,其样本均值为
 ,则总体均值μ的 0.95的置信区间为( )。
,则总体均值μ的 0.95的置信区间为( )。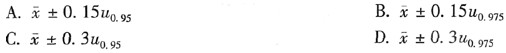 正确答案:B
正确答案:B
解析:由X~N(μ,0.09)可知该总体标准差已知,用正态分布得μ的1-α的置信区间为。所以μ的0.95的置信区间=。 -
第4题:
假设某总体服从正态分布N(12, 4),现从中随机抽取一容量为5的样本X1,X2, X3, X4, X5,则:
样本均值与总体均值之差的绝对值大于1的概率是()。
A. 0.2628 B. 0. 98 C. 0.9877 D. 0.9977答案:A解析:样本均值 服从正态分布N(12,0.8),样本均值与总体均值之差的绝对值大于1的概率为:
服从正态分布N(12,0.8),样本均值与总体均值之差的绝对值大于1的概率为:

-
第5题:
设总体X~N(μ,25),X1,X2,…,X100为来自总体的简单随机样本,求样本均值与总体均值之差不超过1.5的概率答案:解析: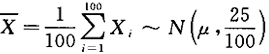 总体均值为E(X)=μ,
总体均值为E(X)=μ,
则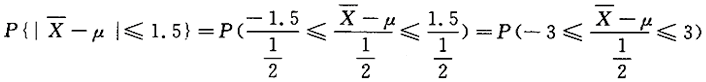
=Ф(3)-Ф(-3)=2Ф(3)-1=0.9973 -
第6题:
设总体X服从正态分布N(μ,σ^2)(σ>0),从该总体中抽取简单随机样本X1,X2,…,Xn(n≥2),其样本均值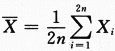 ,求统计量
,求统计量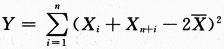 的数学期望E(Y).答案:解析:
的数学期望E(Y).答案:解析: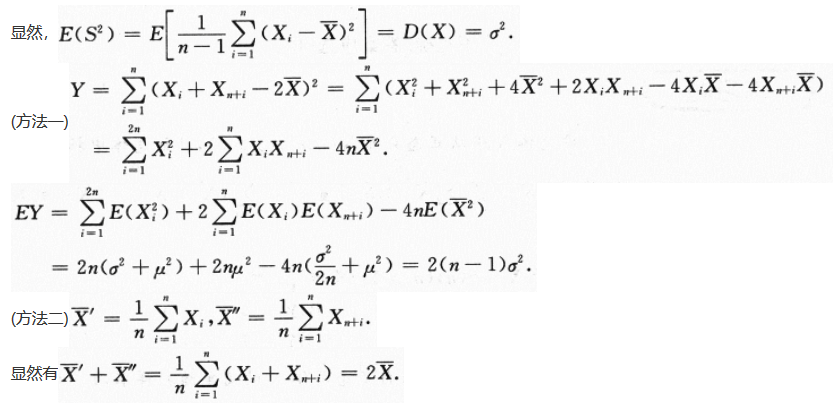
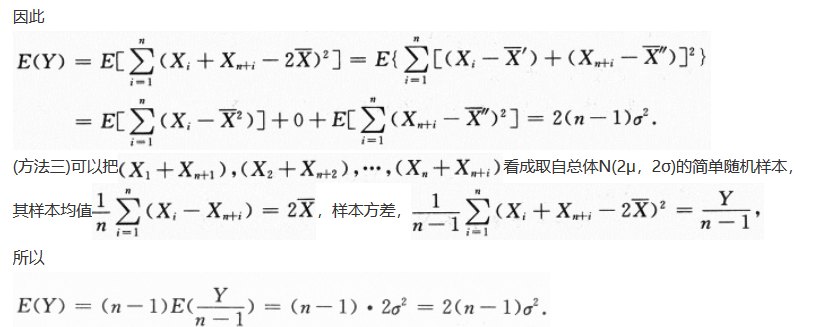
-
第7题:
设总体X服从正态分布N(μ,σ^2)(σ>0),X1,X1,…,Xn为来自总体X的简单随机样本,令Y=.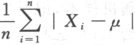 ,求Y的数学期望与方差答案:解析:
,求Y的数学期望与方差答案:解析: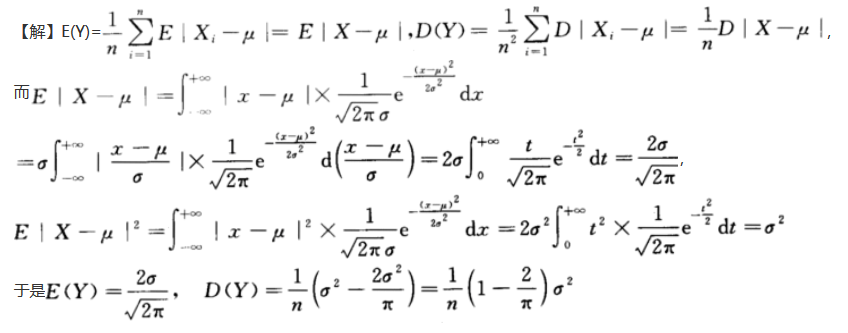
-
第8题:
当总体服从正态分布时,样本均值一定服从正态分布,即有X~N(μ,σ2)时,
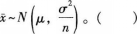 答案:对解析:
答案:对解析: -
第9题:
设某人群的身高X服从N(155.4,5.32)分布,现从该总体中随机抽出一个n=10的样本,得均值为X=158.36,S=3.83,求得μ的95%可信区间为(155.62,161.10),发现该区间竟然没有包括真正的总体均数155.4。若随机从该总体抽取含量n=10的样本200个,每次都求95%置信区间,那么类似上面的置信区间(即不包括155.4在内)大约有().
- A、5个
- B、20个
- C、10个
- D、1个
- E、190个
正确答案:C -
第10题:
关于中心极限定理的描述正确的是:()。
- A、对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布
- B、正态样本均值服从分布N(μ,σ2/n)
- C、设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布
- D、无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
正确答案:A,B,C,D -
第11题:
单选题设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。A服从正态分布N(0,1)
Bn服从正态分布N(0,1)
C服从自由度为n的x2分布
D服从自由度为(n-1)的t分布
正确答案: A解析: 暂无解析 -
第12题:
单选题设某人群的身高X服从N(155.4,5.32)分布,现从该总体中随机抽出一个n=10的样本,得均值为=158.36,S=3.83,求得μ的95%可信区间为(155.62,161.10),发现该区间竟然没有包括真正的总体均数155.4。若随机从该总体抽取含量n=10的样本200个,每次都求95%置信区间,那么类似上面的置信区间(即不包括155.4在内)大约有()A5个
B20个
C10个
D1个
E190个
正确答案: E解析: 暂无解析 -
第13题:
听力原文:对于总体正态分布用选项B,对于样本均值的正态分布,甩选项ACD。
设X~N(μ,σ2),是容量为n的样本均值,s为样本标准差,则下列结论成立的有( )。
 正确答案:ABCD
正确答案:ABCD
-
第14题:
从正态分布总体X~N(μ,σ)中随机取含量为n的样本,样本均数为。服从标准正态分布的随机变量是
A.X-σ
B.X-σX
C.X-μσ
D.X-μσX
E.-μSX
参考答案:C
-
第15题:
设总体X~N(μ,σ^2),X1,X2,…,Xn为总体X的简单随机样本,X与S^2分别为样本均值与样本方差,则(). 答案:A解析:
答案:A解析: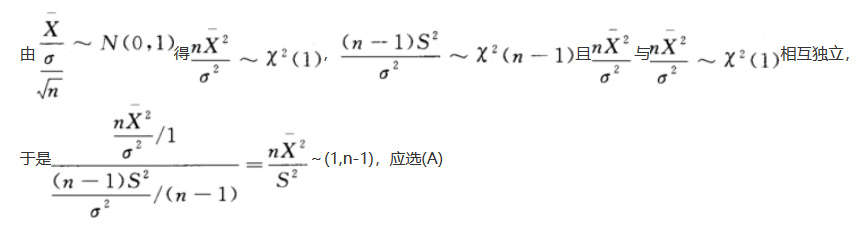
-
第16题:
设总体X服从参数为2的指数分布,X1,X2,…,Xn为来自总体X的简单随机样本,则当n→∞时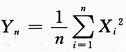 ,依概率收敛于_______.答案:解析:本题是数三的考题,根据切比雪夫大数定律或者辛钦大数定律
,依概率收敛于_______.答案:解析:本题是数三的考题,根据切比雪夫大数定律或者辛钦大数定律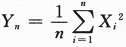 ,依概率收敛于
,依概率收敛于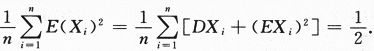 答案应填
答案应填
-
第17题:
设总体X服从分布N(0,2^2),而X1,X2,…,X15是来自总体X的简单随机样本,则随机变量 服从_______分布,参数为________.答案:1、F 2、(10,5)解析:本题是数三的考题,由于X~N(0,2^2),则
服从_______分布,参数为________.答案:1、F 2、(10,5)解析:本题是数三的考题,由于X~N(0,2^2),则
且相互独立,故
答案应填服从F分布,参数为(10,5). -
第18题:
设总体X~N(0,2^2),X1,X2,…,X30为总体X的简单随机样本,求统计量U=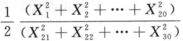 所服从的分布及自由度.答案:解析:
所服从的分布及自由度.答案:解析:
-
第19题:
设总体X~N(u,σ2),基于来自总体X的容量为16的简单随机样本,测得样本均值x= 31.645,样本方差S2=0.09,则总体均值μ的置信度为0.98的置信区间为( )。
A.(30.88, 32.63)
B.(31.45, 31.84)
C.(31.62, 31.97)
D.(30.45, 31.74)答案:B解析:
-
第20题:
从均值为μ,方差为σ2的任意一个总体中抽取大小为n的样本,则()
- A、当n充分大时,样本均值的分布近似服从正态分布
- B、只有当n<30时,样本均值的分布近似服从正态分布
- C、样本均值的分布与n无关
- D、无论n多大,样本均值的分布都是非正态分布
正确答案:A -
第21题:
设(X1,X2,…,X)是抽自正态总体N(0,1)的一个容量为n的样本,记,则下列结论中正确的是()。
- A、服从正态分布N(0,1)
- B、n服从正态分布N(0,1)
- C、服从自由度为n的x2分布
- D、服从自由度为(n-1)的t分布
正确答案:C -
第22题:
多选题关于中心极限定理的描述正确的是:()。A对于n个相互独立同分布的随机变量共同服从正态分布,则样本均值又仍为正态分布
B正态样本均值服从分布N(μ,σ2/n)
C设X1,X2,„,Xn为n个相互独立共同分布随机变量,其共同分布不为正态分布或未知,但其均值和方差都存在,则在n相当大时,样本均值近似服从正态分布
D无论共同分布是什么,只要变量个数n相当大时,均值的分布总近似于正态分布
正确答案: C,D解析: 暂无解析 -
第23题:
单选题从均值为μ,方差为σ2的任意一个总体中抽取大小为n的样本,则()A当n充分大时,样本均值的分布近似服从正态分布
B只有当n<30时,样本均值的分布近似服从正态分布
C样本均值的分布与n无关
D无论n多大,样本均值的分布都是非正态分布
正确答案: D解析: 暂无解析 -
第24题:
单选题设某人群的身高X服从N(155.4,5.32)分布,现从该总体中随机抽出一个n=10的样本,得均值为X=158.36,S=3.83,求得μ的95%可信区间为(155.62,161.10),发现该区间竟然没有包括真正的总体均数155.4。若随机从该总体抽取含量n=10的样本200个,每次都求95%置信区间,那么类似上面的置信区间(即不包括155.4在内)大约有( )。A5个
B20个
C10个
D1个
E190个
正确答案: B解析:
μ的95%置信区间意味着100次随机抽样会有5次不包含μ的机会,200次随机抽样会有10次不包含μ的机会。
