问答题相贯线的求作条件、求相贯线的步骤？

题目
问答题
相贯线的求作条件、求相贯线的步骤？
相似考题

1.当相贯体被某一投影面的平行面截切,所得各形体的截交线均为规则图形,该相贯线的求作应选用()。A、切线法B、素线法C、辅助平面法D、辅助球面法

2.切线法求相贯线适用于划()类形体相交的相贯线。A、圆柱、圆球B、圆锥、圆球C、圆锥、棱柱D、圆柱、圆锥

3.在求相贯线特殊点时,一定要特别注意相贯线轮廓的()。A、等分点B、折点C、交点D、起始点

4.底面水平的圆锥体与水平位置的圆柱体相贯,求作其相贯线的作图方法是(),相贯线上各交点是在水平投影面上求得。A、切线法B、素线法C、辅助平面法D、辅助球面法

参考答案和解析
正确答案： 两个几何体无缝隙的连接或结合称为相贯，相贯线是指两个几何体在相交部位的结合线，因此，相贯线上的每个点都是两个几何体上共有的点，这是求作相贯线的基本条件。
求作相贯线的基本步骤是：先找出特殊相贯点（如圆的象限点、最高最低点、最左最右点、最前最后点、可见部分与不可见部分的分界点等）；再在这些特殊相贯点之间找出适当数量的相贯点（点越多相贯线就越精确）；最后用平滑的曲线将这些点连接起来。因此，求作相贯线的关键是找相贯点。在曲面上找点的最常用的方法有素线法和纬圆法。
解析： 暂无解析
更多“相贯线的求作条件、求相贯线的步骤？”相关问题

  • 第1题：

    辅助平面法求相贯线实质上也是在求一系列(),进而连接出相贯线的。

    A、特殊点

    B、等分点

    C、一般点

    D、相贯点


    参考答案：D

  • 第2题：

    特殊点法求相贯线可适用于任何形体相交的相贯线。()

    此题为判断题(对，错)。


    参考答案：正确

  • 第3题：

    辅助截面法求相贯线实质上是在求一系列(),进而连接出相贯线的。

    A、特殊点

    B、交点

    C、相贯线


    参考答案：C

  • 第4题：

    辅助截面法求相贯线实质上也是在求一系列(),进而连接出相贯线。

    A.特殊点

    B.交点

    C.相贯线


    参考答案：C

  • 第5题：

    关于辅助平面法求相贯线的投影,下面哪些说法是正确的()?

    A.辅助平面应该与相贯线相交或相切，也与两个相贯立体相交或相切

    B.辅助平面应该与相贯线相交，但不必要与两个相贯立体都相交

    C.辅助平面与相贯体产生的交线的投影应该尽可能简单好求，比如是直线或圆


    参考答案：AC

  • 第6题：

    27：求相贯线的主要方法有哪些？


    正确答案：

     

    有素线法，辅助平面法，球面法。

  • 第7题：

    求相贯线方法的选择原则是什么?


    正确答案：用素线法求相贯线至少应已知相贯线的一个投影;用辅助平面法求相贯线，截交线应是最简单的几何图形;球面法只适用于回转体相贯，且轴线相交的构件。

  • 第8题：

    相贯线的求作条件、求相贯线的步骤？


    正确答案: 两个几何体无缝隙的连接或结合称为相贯，相贯线是指两个几何体在相交部位的结合线，因此，相贯线上的每个点都是两个几何体上共有的点，这是求作相贯线的基本条件。
    求作相贯线的基本步骤是：
    先找出特殊相贯点（如圆的象限点、最高最低点、最左最右点、最前最后点、可见部分与不可见部分的分界点等）；
    再在这些特殊相贯点之间找出适当数量的相贯点（点越多相贯线就越精确）；
    最后用平滑的曲线将这些点连接起来。因此，求作相贯线的关键是找相贯点。在曲面上找点的最常用的方法有素线法和纬圆法。

  • 第9题：

    底面水平的圆锥体与水平位置的圆柱体相贯，求作其相贯线的作图方法是（）相贯线上各交点是在水平投影面上求得。

    • A、切线法
    • B、取点法
    • C、辅助平面法
    • D、辅助球面

    正确答案:C

  • 第10题：

    当相贯体被某一投影面的平行线截切，所得各形体的截交线均为规则图形，该相贯线的求作应选用（）。

    • A、切线法
    • B、取点法
    • C、辅助平面法
    • D、辅助球面法

    正确答案:D

  • 第11题：

    求相贯线的主要方法是什么？


    正确答案: 是辅助平面法、素线法、球面法。

  • 第12题：

    问答题
    相贯线的求作条件、求相贯线的步骤？

    正确答案： 两个几何体无缝隙的连接或结合称为相贯，相贯线是指两个几何体在相交部位的结合线，因此，相贯线上的每个点都是两个几何体上共有的点，这是求作相贯线的基本条件。
    求作相贯线的基本步骤是：
    先找出特殊相贯点（如圆的象限点、最高最低点、最左最右点、最前最后点、可见部分与不可见部分的分界点等）；
    再在这些特殊相贯点之间找出适当数量的相贯点（点越多相贯线就越精确）；
    最后用平滑的曲线将这些点连接起来。因此，求作相贯线的关键是找相贯点。在曲面上找点的最常用的方法有素线法和纬圆法。
    解析： 暂无解析

  • 第13题：

    求作轴线相交的圆柱与圆锥表面的相贯线时采用了球面法,因此说,所求得的相贯线均在同一球面上。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第14题：

    切线法求相贯线可适用于划()类形体相交的相贯线。

    A、圆柱、圆球

    B、圆锥、圆球

    C、圆柱、圆锥


    参考答案：C

  • 第15题：

    用辅助球面法求相贯线时必须满足哪两个条件?


    正确答案：满足一是回转体相贯，二是回转体的轴线要相交且要反映实长。

  • 第16题：

    我们在求作轴线相交的圆柱与圆锥表面的相贯线时采用了球面法,因此说,所求得的相贯线均在同一球面上。()

    此题为判断题(对，错)。


    参考答案：正确

  • 第17题：

    求作圆柱与圆锥体的相贯线。


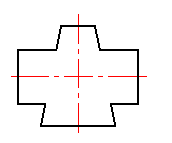    正确答案：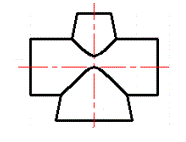

  • 第18题：

    94：求相贯线方法的选择原则是什么？


    正确答案：

     

    用素线法求相贯线至少应已知相贯线的一个投影；用辅助平面法求相贯线，截交线应是最简单的几何图形；球面法只适用于回
    转体相贯，且轴线相交的构件。

  • 第19题：

    关于相贯线，下面说法正确的是（）

    • A、相贯线是相交两形体表面的共有线
    • B、相贯线是相交两形体的分界线
    • C、相贯线都是封闭的
    • D、求相贯线的方法主要有素线法、辅助平面法和辅助球面法

    正确答案:A,B,C,D

  • 第20题：

    辅助截面法求相贯线实质上也是在求一系列（），进而连接出相贯线。

    • A、特殊点
    • B、交点
    • C、相贯线

    正确答案:C

  • 第21题：

    表面取点法求作相贯线的一般步骤是什么？


    正确答案: ①分析：首先分析两曲面立体的几何形状、相对大小和相对位置，进一步分析相贯线是空间曲线，还是处于特殊情况（平面曲线或直线）。分析两曲面立体对投影面的相对位置，两曲面立体的投影是否有积聚性，哪个投影有积聚性。分析相贯线哪个投影是已知的，哪个投影是要求作的。
    ②求特殊点：相贯线上的特殊点包括极限位置点、轮廓转向点、曲线特征点和结合点四种。
    ③根据需要求出若干个一般点。
    ④判别可见性，顺次光滑连接各点，作出相贯线。
    ⑤补全可见与不可见部分的轮廓线或转向轮廓线，并擦除被切割掉的轮廓线

  • 第22题：

    求相贯线的实质是什么？


    正确答案: 就是在两形体表面上找出一定数量的共有点，将这些共有点依次连接起来即为所求。

  • 第23题：

    球面法求相贯线的方法是用截平面通过内截切（）以获得共有点求出相贯线。

    • A、相贯体
    • B、多面体
    • C、组合体
    • D、形体

    正确答案:A

  • 第24题：

    问答题
    表面取点法求作相贯线的一般步骤是什么？

    正确答案： ①分析：首先分析两曲面立体的几何形状、相对大小和相对位置，进一步分析相贯线是空间曲线，还是处于特殊情况（平面曲线或直线）。分析两曲面立体对投影面的相对位置，两曲面立体的投影是否有积聚性，哪个投影有积聚性。分析相贯线哪个投影是已知的，哪个投影是要求作的。
    ②求特殊点：相贯线上的特殊点包括极限位置点、轮廓转向点、曲线特征点和结合点四种。
    ③根据需要求出若干个一般点。
    ④判别可见性，顺次光滑连接各点，作出相贯线。
    ⑤补全可见与不可见部分的轮廓线或转向轮廓线，并擦除被切割掉的轮廓线
    解析： 暂无解析

相关内容