单选题关于x的不等式x－b＞0恰有两个负整数解，则b的取值范围是（　　）．A －3＜b＜－2B －3＜b≤－2C －3≤b≤－2D －3≤b＜－2

题目
单选题
关于x的不等式x－b＞0恰有两个负整数解，则b的取值范围是（　　）．
A

－3＜b＜－2

B

－3＜b≤－2

C

－3≤b≤－2

D

－3≤b＜－2

相似考题

1.如果Sgn(x)的值为-1，整型变量x的值是( )。A、 0B、 整数C、 正整数D、 负整数

2.求不等式5（x-2）≤28+2x的正整数解。

3.在0、-4、3、-3、1/5、-5、4、-10中，______是方程x+4=0的解；______是不等式x+4≥0的解；______是不等式x+4＜0的解。）比较a与2a的大小。

4.在不等式ax+b＞0中，a，b是常数，且a≠0。当______时，不等式的解集是x＞-b/a； 当______时，不等式的解集是x＜- b/a。

更多“关于x的不等式x－b＞0恰有两个负整数解，则b的取值范围是（　　）．”相关问题

  • 第1题：

    求不等式4（x+1)≤64的正整数解。


    正整数解有1,2,3,...,14,15


  • 第2题：

    关于x的方程2cos2x-sinx+a0在区间[0，7π/6]上恰好有两个不等实根，则实数a的取值范围是_____。


    答案：
    解析：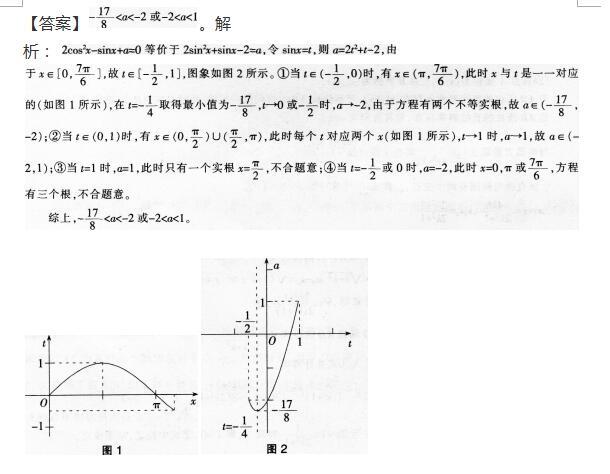

  • 第3题：

    若不等式x2-x≤0的解集为M，函数?(x)=In(1-|x|)的定义域为N，则M∩N为()．?

    A.[0，1)
    B.(0，1)
    C.[0，1]
    D.(-1，0]

    答案：A
    解析：
    M={x|x2-x≤0}={x{0≤x≤1}，N={x|1-|x|>0}={x|-1

  • 第4题：

    若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等实根，则k的取值范围( )。


    答案：C
    解析：

  • 第5题：

    一对互为对偶的问题存在最优解，则在其最优点处有（）

    • A、若某个变量取值为0，则对应的对偶约束为严格的不等式
    • B、若某个变量取值为正，则相应的对偶约束必为等式
    • C、若某个约束为等式，则相应的对偶变取值为正
    • D、若某个约束为严格的不等式，则相应的对偶变量取值为0
    • E、若某个约束为等式，则相应的对偶变量取值为0

    正确答案:B,D

  • 第6题：

    假设考试成绩的取值范围为0～150的整数，则最合适的数据类型是（）。

    • A、.int
    • B、numeric（4，1）
    • C、tinyint
    • D、numeric（3，0）

    正确答案:C

  • 第7题：

    以下对广东农村信用社系统中转移参数设置的取值范围描述正确的是（）

    • A、取值范围为0%到100%的正整数
    • B、取值范围为0%到200%的正整数
    • C、取值范围为0%到300%的正整数
    • D、取值范围为0%到400%的正整数

    正确答案:D

  • 第8题：

    填空题
    能够使不等式(|x|－x)(1＋x)＜0成立的x的取值范围是____．

    正确答案： x<-1
    解析：
    当x≥0时，|x|－x＝x－x＝0，于是(|x|－x)(1＋x)＝0，不满足原式，故舍去x≥0．
    当x＜0时，|x|－x＝－2x＞0，x应当要使(|x|－x)(1＋x)＜0，满足1＋x＜0，即x＜－1，所以x的取值范围是x＜－1．

  • 第9题：

    多选题
    一对互为对偶的问题存在最优解，则在其最优点处有（）
    A

    若某个变量取值为0，则对应的对偶约束为严格的不等式

    B

    若某个变量取值为正，则相应的对偶约束必为等式

    C

    若某个约束为等式，则相应的对偶变取值为正

    D

    若某个约束为严格的不等式，则相应的对偶变量取值为0

    E

    若某个约束为等式，则相应的对偶变量取值为0


    正确答案： D,C
    解析： 暂无解析

  • 第10题：

    单选题
    以下对广东农村信用社系统中转移参数设置的取值范围描述正确的是（）
    A

    取值范围为0%到100%的正整数

    B

    取值范围为0%到200%的正整数

    C

    取值范围为0%到300%的正整数

    D

    取值范围为0%到400%的正整数


    正确答案： D
    解析： 暂无解析

  • 第11题：

    填空题
    若不等式x2－ax－b＜0的解集是{x|2＜x＜3}，则a＋b＝____．

    正确答案： -1
    解析：
    由题可知，2和3应为方程x2－ax－b＝0的两个根．根据根与系数的关系，2＋3＝a，2×3＝－b，即a＝5，b＝－6．a＋b＝－1．

  • 第12题：

    单选题
    如果线性规划问题有可行解，那么该解必须满足（）
    A

    所有约束条件

    B

    变量取值非负

    C

    所有等式要求

    D

    所有不等式要求


    正确答案： C
    解析： 暂无解析

  • 第13题：

    不等式2(x-2)≤x-2的非负整数解的个数为().?

    A.1
    B.2
    C.3
    D.4

    答案：C
    解析：
    解2(x-2)≤x-2得x≤2，故非负整数解为0，1，2，即有3个.

  • 第14题：

    不等式2x2+3mx+2m>0的解集是实数集，则m的取值范围是( )



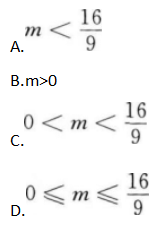    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为不等式的解集． 【应试指导】由2x2+3mx+2m>0的解集为R，又因为抛物线的开口向上，所以方程2x2+3mx+2m=0无实根，

  • 第15题：


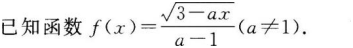
    (1)若a>0，则?(x)的定义域是__________；
    (2)若?(x)在区间(0，1]上是减函数，则实数a的取值范围是__________．


    答案：
    解析：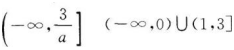


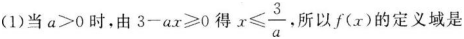
  • 第16题：

    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。


    正确答案: 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1

  • 第17题：

    如果线性规划问题有可行解，那么该解必须满足（）

    • A、所有约束条件
    • B、变量取值非负
    • C、所有等式要求
    • D、所有不等式要求

    正确答案:D

  • 第18题：

    传递函数G（s）的零点是（）

    • A、G（s）=0的解
    • B、G（s）=∞的解
    • C、G（s）＞0的不等式解
    • D、G（s）＜0的不等式解

    正确答案:A

  • 第19题：

    单选题
    如果Sgn（x）的值为-1整型变量x的值是（）。
    A

    0

    B

    整数

    C

    正整数

    D

    负整数


    正确答案： A
    解析： 暂无解析

  • 第20题：

    单选题
    n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX=O有两个线性无关的解，则（　　）.
    A

    A*X=0的解均是AX=0的解

    B

    AX=0的解均是A*X=O的解

    C

    AX=0与A*X=0无非零公共解

    D

    AX=0与A*X=O仅有2个非零公共解


    正确答案： B
    解析：
    由齐次方程组AX=0有两个线性无关的解向量，知方程组AX=0的基础解系所含解向量的个数为n-r（A）≥2，即r（A）≤n-2<n-1．由矩阵A与其伴随矩阵秩的关系，知r（A*）=0，即A*=0．所以任意n维列向量均是方程组A*X=0的解，故方程组AX=0的解均是A*X=0的解．

  • 第21题：

    单选题
    传递函数G（s）的零点是（）
    A

    G（s）=0的解

    B

    G（s）=∞的解

    C

    G（s）＞0的不等式解

    D

    G（s）＜0的不等式解


    正确答案： D
    解析： 暂无解析

  • 第22题：

    问答题
    已知p：方程x2+mx+1=0有两个不等负实根。q：方程4x2+4（m-2）x+1=0无实根。若p或q为真，p且q为假。求实数m的取值范围。

    正确答案： 因为p或q为真，p且q为假，则必然p与q中有一真一假。分两种情况：p为真，q为假；q为真，p为假。
    （1）若p为真，则q为假。
    p为真，方程x2+mx+1=0有两个不等负实根成立，即△=m2-4>0，x+x=m<0，解得：m>2或m<-2，m>0。综上两式得到：m>2。
    q为假，方程4x2+4（m-2）x+1=0无实根不成立，即有实数根，△=16（m-2）2-16≥0，所以m≥3或m≤1。
    取交集得到，m≥3：
    （2）若q为真，则p为假。
    q为真，即方程4x2+4（m-2）x+1=0无实根成立，即△=16（m-2）2-16<0，所以1p为假，方程x2+mx+1=0有两个不等负实根不成立，即①无实根或有两个相等实根，△=m2-4≤0，或②有两个不等正实根，△=m2-4>0，x+x=-m>0。解得，①-2≤m≤2或②m<-2，所以m≤2。
    取交集得到：1综上所述m≥3或1
    解析： 暂无解析

  • 第23题：

    单选题
    n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX(→)＝0(→)有两个线性无关的解，则（　　）。
    A

    A*X(→)＝0(→)的解均是AX(→)＝0(→)的解

    B

    AX(→)＝0(→)的解均是A*X(→)＝0(→)的解

    C

    AX(→)＝0(→)与A*X(→)＝0(→)无非零公共解

    D

    AX(→)＝0(→)与A*X(→)＝0(→)仅有2个非零公共解


    正确答案： A
    解析：
    由齐次方程组AX(→)＝0(→)有两个线性无关的解向量，知方程组AX(→)＝0(→)的基础解系所含解向量的个数为n－r（A）≥2，即r（A）≤n－2＜n－1。由矩阵A与其伴随矩阵秩的关系，知r（A*）＝0，即A*＝0。所以任意n维列向量均是方程组A*X(→)＝0(→)的解，故方程组AX(→)＝0(→)的解均是A*X(→)＝0(→)的解。

相关内容