单选题随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（）为3/10。A 出现正面的频数B 出现正面的频率C 出现正面的概率D 出现正面的可能性

题目
单选题
随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（）为3/10。
A

出现正面的频数

B

出现正面的频率

C

出现正面的概率

D

出现正面的可能性

相似考题

1.将一枚硬币投掷两次，至少出现一次正面的概率为（ ）。A．0.25B．0.50C．0.75D．1.00

2.扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的( )。A．古典概率方法B．统计概率方法C．主观概率方法D．样本概率方法

3.一枚硬币掷3次,出现两次或两次以上正面的概率是()。A.0.1B.0.9C.0.8D.0.5

4.独立地抛掷一枚质量均匀硬币,已知连续出现了10次反面,问下一次抛掷时出现的是正面的概率是:()A、1/11B、B.1/10C、C.1/2D、D.1/9

参考答案和解析
正确答案： C
解析： 暂无解析
更多“单选题随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（）为3/10。A 出现正面的频数B 出现正面的频率C 出现正面的概率D 出现正面的可能性”相关问题

  • 第1题：

    抛掷一枚硬币，观察其出现正面或反面的过程，就是随机试验，“正面向上”就是随机事件。()


    参考答案：正确

  • 第2题：

    （2）连续4次抛掷一枚硬币，求恰出现两次是正面的概率和最后两次出现是正面的概率。


    正确答案：
              

  • 第3题：

    随机投一枚硬币共10 次，其中3 次为正面， 7 次为反面。则该随机事件( )为3/10，

    A.出现正面的频数
    B. 出现正面的频率
    C. 出现正面的概率
    D.出现正面的可能性

    答案：B
    解析：

  • 第4题：

    扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的()。

    A:古典概率方法
    B:统计概率方法
    C:主观概率方法
    D:样本概率方法

    答案：A
    解析：

  • 第5题：

    正平面的正面投影积聚为直线。()


    答案：错
    解析：

  • 第6题：

    将一枚硬币投掷两次，至少出现一次正面的概率为（ ）。
    A. 0. 25 B. 0.50 C. 0.75 D. 1.00


    答案：C
    解析：

  • 第7题：

    一枚硬币被扔了三次，如果三次都是正面，此时第四次出现正面的概率是（）。

    • A、0
    • B、1/16
    • C、1/2
    • D、大于背面的概率

    正确答案:C

  • 第8题：

    一枚硬币被投掷三次并且三次都是正面，第四次试验出现正面的概率（）

    • A、比出现背面的概率小
    • B、比出现背面的概率大
    • C、是1/16
    • D、是1/2

    正确答案:D

  • 第9题：

    一枚硬币被投掷6次，6次都是背面，那么在第七次投掷中（）

    • A、不可能出现背面
    • B、出现正面的可能性大于背面
    • C、出现背面的可能性大于正面
    • D、以上均错误

    正确答案:D

  • 第10题：

    抛3枚硬币，出现3次正面的概率为（）。

    • A、0.12
    • B、0.15
    • C、0.25
    • D、0.125

    正确答案:D

  • 第11题：

    单选题
    下列事件中，必然事件是(　　)．
    A

    掷一枚硬币出现正面    

    B

    掷一枚硬币出现反面

    C

    掷一枚硬币，或者出现正面，或者出现反面  

    D

    掷一枚硬币，出现正面和反面


    正确答案： A
    解析： 根据必然事件的定义可以知道

  • 第12题：

    判断题
    正平面的正面投影积聚为直线。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第13题：

    投一枚硬币三次，问恰好有两次正面一次反面的概率是多少？（ ）

    A．4/5

    B．2/3

    C．3/8

    D．1/2


    正确答案：C
    一枚硬币投三次共有8种结果，用1表示为正面，0表示反面，则有(0，0，0)，(0，0，1)，(0，1，0)，(1，0，0)，(1，1，0)，(1，0，1)，(0，1，1)，(1，1，1)种结果，可以看到满足条件的结果有3种，概率是3/8。

  • 第14题：

    随机投一枚硬币共10次，其中3次为正面，7次为反面。则该随机事件（ ）为3/10。

    A：出现正面的频数
    B：出现正面的频率
    C：出现正面的概率
    D：出现正面的可能性

    答案：B
    解析：

  • 第15题：

    设X和Y分别表示扔n次硬币出现正面和反面的次数,则X,Y的相关系数为().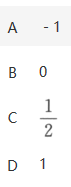


    答案：A
    解析：
    设正面出现的概率为p，则X～B（n，p），Y=n-X～B（n，1-p），E(X)=np,D(X)=np(1-p),E(Y)=n(1-p),D(Y)=np(1-p),Cov(X，Y)=Cov(X，n-X)=Cov(X，n)-Cov(X，X)，因为Cov(X,n)=E(nX)-E（n）E(X)=nE(X)-nE(X)=0,Cov(X，X)=D(X)=np（1-p），所以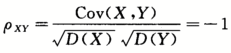，选(A)

  • 第16题：

    计算以下事件的概率可以用古典概率方法解决的是()。

    A:明天是晴天的概率
    B:抛一枚硬币出现正面的概率
    C:明天股票上涨的概率
    D:某地发生交通事故的概率

    答案：B
    解析：
    可以使用古典概率方法计算概率的事件需具备三个条件：事件可能产生的结果是有限的，所有结果之间两两互不相容的，所有的结果发生都是等可能的。依据这三个条件，只有B项符合。

  • 第17题：

    假设扔一枚质地均匀的硬币，我们知道出现正面或反面的概率都是0.5，这属于概率应用方法中的()。

    A:古典概率方法
    B:先验概率方法
    C:主观概率方法
    D:样本概率方法
    E:统计概率方法

    答案：A,B
    解析：
    可用古典概率或先验概率方法进行计算的随机现象应同时具有以下特征：①在试验中它的全部可能结果是有限的，并且这些事件是两两互不相容的；②各事件的发生或出现是等可能的。本题中，扔硬币出现的可能结果的范围仅限于正面或反面，并且结果的出现具有等可能性。

  • 第18题：

    连抛一枚均匀硬币4次，既有正面又有反面的概率为（ ）。
    A. 1/16 B. 1/8 C. 5/8 D. 7/8


    答案：D
    解析：
    连抛硬币4次可重复排列数为：n=24= 16。而全是正面或全是反面各1种可能，所以既有正面又有反面的有：k = 16－2 =14种可能。故“既有正面又有反面”的概率为：P（A） =k/n=7/8。

  • 第19题：

    将一枚硬币连抛两次，则此随机试验的样本空间为（）

    • A、{（正，正），（反，反），（一正一反）}
    • B、{（反，正），（正，反），（正，正），（反，反）}
    • C、{一次正面，两次正面，没有正面}
    • D、{先得正面，先得反面}

    正确答案:B

  • 第20题：

    抛掷一枚均匀的硬币，出现正面的概率是（）。

    • A、0
    • B、1
    • C、0.5
    • D、0.8

    正确答案:C

  • 第21题：

    一枚一角硬币被扔了四次，如果四次全是背面，此时扔第五次出现正面的可能性是（）。

    • A、小于出现背面的概率
    • B、大于出现背面的概率
    • C、1/2
    • D、1/32

    正确答案:C

  • 第22题：

    单选题
    抛3枚硬币，出现3次正面的概率为（）。
    A

    0.12

    B

    0.15

    C

    0.25

    D

    0.125


    正确答案： D
    解析： 抛3枚硬币一共会出现8种结果，全为正面是其中的一种，概率为1÷8=0.125

  • 第23题：

    单选题
    连抛一枚均匀硬币4次，既有正面又有反面的概率为（　　）。
    A

    1/16

    B

    1/8

    C

    5/8

    D

    7/8


    正确答案： C
    解析： 连抛硬币4次可重复排列数为:n＝24＝16。而全是正面或全是反面各1种可能，所以既有正面又有反面的有:k＝16-2＝14种可能。故“既有正面又有反面”的概率为:P（A）＝k/n＝7/8。

相关内容