问答题8.袋中有7个球，其中红球5个白球2个，从袋中取球两次，每次随机地取一个球，取后不放回，求： (1)第一次取到白球、第二次取到红球的概率； (2)两次取得一红球一白球的概率．

第1题：

第2题：

第3题：

答案：

解析：

一般理解随机事件“第二个人取得黄球”与第一个人取得的是什么球有关，这就要用全概率公式来计算，但也可以用古典型概率来解，这会简单得多.(方法一)设事件Ai表示第i个人取得黄球，i=1，2，则根据全概率公式：

(方法二)只考虑第二个人取得的球，这50个球中每一个都会等可能地被第二个人取到，而取到黄球的可能有20个，故所求概率为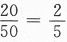

第4题：

答案：

解析：

方法一基本事件数n=（a+b）!，设Ak={第k次取到黑球），则有利样本点数为a(a+b-1)!，所以

方法二把所有的球看成不同对象，取k次的基本事件数为，第k次取到黑球所包含的事件数为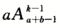，则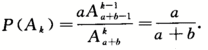

第5题：

袋中有10个大小相等的球,其中6个红球4个白球,随机抽取2次,每次取1个,定义两个随机变量如下：
　　
　　就下列两种情况,求(X,Y)的联合分布律：
　　(1)第一次抽取后放回；(2)第一次抽取后不放回.

答案：

解析：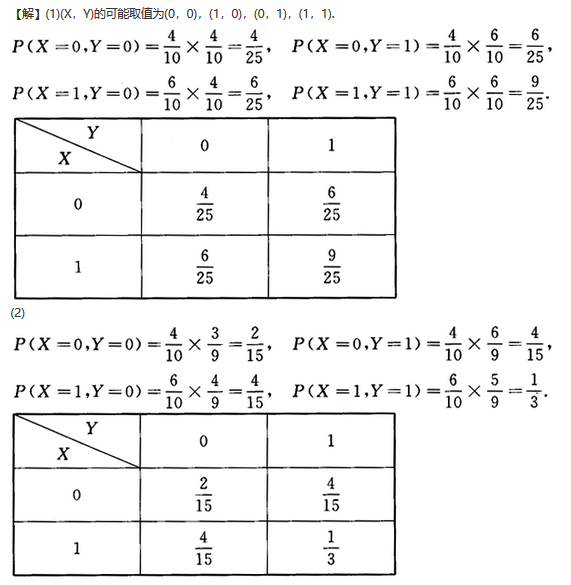

第6题：

袋中有50个球，其中20个新球，30个旧球，现每次取1球，无放回地取2次，则第2次取得旧球的概率是()。

第7题：

答案：

解析：

第8题：

袋中有l个红球、2个黑球与3个白球，现有放回地从袋中取两次，每次取一个球，以X，y，Z分别表示两次取球所取得的红球、黑球与白球的个数。
(1)求
(2)求二维随机变量(X，Y)的概率分布。

答案：

解析：

第9题：

答案：

解析：

第10题：

第11题：

设袋中有2个黑球、3个白球，有放回地连续取2次球，每次取一个，则至少取到一个黑球的概率是（）

第12题：

第13题：

答案：B

解析：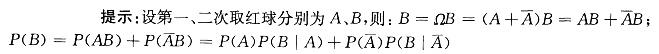

或“试验分两步，求第二步结果的概率”用全概率公式。

第14题：

答案：

解析：

【解】(1)设A1={一次性抽取4个球，其中2个红球2个白球），则
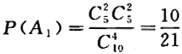
(2)设A2={逐个抽取4个球，取后不放回，其中2个红球2个白球}，则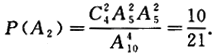

(3)设A3={逐个抽取4个球，取后放回，其中2个红球2个白球}，则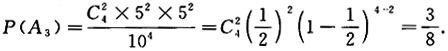

第15题：

答案：

解析：

设A1={第一次取红球)，A2={第一次取白球），B={第二次取红球），　　

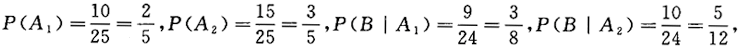
则
　　

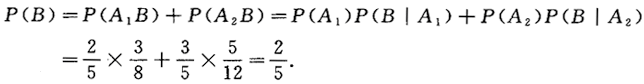
第16题：

袋中有一个红球，两个黑球，三个白球，现在放回的从袋中取两次，每次取一个，求以X、Y、Z分别表示两次取球所取得的红、黑与白球的个数。①求②求二维随机变量(X,Y)的概率分布。

答案：

解析：

第17题：

答案：

解析：

第18题：

答案：

解析：

第19题：

第20题：

答案：

解析：

第21题：

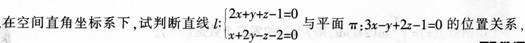
袋子中有70个红球，30个黑球，从袋子中连续摸球两次，每次摸一个球，且第一次摸出的球，不放回袋中：
(1)求两次摸球均为红球的概率：
(2)若第一次摸到红球，求第二次摸到黑球的概率。

答案：

解析：

平面π的法向量为n=(3，-1，2)；

第22题：

袋中共有5个球，其中3个新球，2个旧球，每次取1个，无放回地取2次，则第二次取到新球的概率是（）．

• A、3/5
• B、3/4
• C、1/2
• D、3/10

第23题：

第24题：