单选题当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年的看跌期权的价格所用的风险中性概率为（）A 0.59B 0.65C 0.75D 0.5
题目
单选题
当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年的看跌期权的价格所用的风险中性概率为（）
A
0.59
B
0.65
C
0.75
D
0.5
相似考题
更多“单选题当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年的看跌期权的价格所用的风险中性概率为（）A 0.59B 0.65C 0.75D 0.5”相关问题
-
第1题：
假设A公司目前的股票价格为20元/股，有1股以该股票为标的资产的看涨期权，到期时间为6个月，执行价格为24元， 6个月内公司不派发股利，预计半年后股价有两种可能，上升30%或者下降23%，半年的无风险利率为4%。
要求：（1）用复制原理计算该看涨期权的价值。
（2）用风险中性原理计算该看涨期权的价值。
（3）如果该看涨期权的现行价格为2.5元，请根据套利原理，构建一个投资组合进行套利。答案：解析：（1）复制原理：
上行股价＝20×（1＋30%）＝26（元）
下行股价＝20×（1－23%）＝15.4（元）
套期保值比率H
＝[（26－24）－0]/（26－15.4）＝0.1887
借款数额＝（0.1887×15.4－0）/（1＋4%）＝2.7942（元）
购买股票支出＝0.1887×20＝3.774（元）
期权价值＝3.774－2.7942＝0.98（元）
（2）风险中性原理：
4%＝上行概率×30%＋（1－上行概率）×（－23%）
求得：上行概率＝0.5094
下行概率＝1－0.5094＝0.4906
期权到期时价值
＝0.5094×（26－24）＋0.4906×0
＝1.0188（元）
期权价值＝1.0188/（1＋4%）＝0.98（元）
（3）由于期权价格高于期权价值，因此，套利过程如下：买入0.1887股股票，借入款项2.7942元，同时卖出1股看涨期权，收到2.5元。
结果获利＝2.5＋2.7942－0.1887×20＝1.52（元）。 -
第2题：
（2015年）甲公司股票当前每股市价40 元，6 个月以后股价有两种可能，上升25%或下降20%，市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权，每份看涨期权可以买入1 股股票，每份看跌期权可以卖出1 股股票，两种期权执行价格均为45 元，到期时间均为6 个月，期权到期前，甲公司不派发现金股利，半年无风险报酬率为2%。
要求：
（1）假设市场上每份看涨期权价格为2.5 元，每份看跌期权价格1.5 元，投资者同时卖出一份看涨期权和一份看跌期权，计算确保该组合不亏损的股票价格区间，如果6 个月后的标的股票价格实际上涨20%，计算该组合的净损益。（注：计算股票价格区间和组合净损益时，均不考虑期权价格的货币时间价值）。
（2）利用风险中性原理，计算看涨期权的股价上行时到期日价值、上行概率及期权价值，利用看涨期
权—看跌期权平价原理，计算看跌期权的期权价值。答案：解析：(1)卖出看涨期权的净损益=—Ma*(股票市价—执行价格，0)+期权价格=—Ma*(股票市价—45，0)+2.5
卖出看跌期权的净损益=—Ma*(执行价格—股票市价，0)+期权价格=—Ma*(45-股票市价，0)+1.5
组合净损益=—Ma*(股票市价-45,0)—Ma*(45-股票市价，0)+4
当股价大于执行价格时：
组合净损益=—(股票市价-45)+4
根据组合净损益=0 可知，股票市价=49(元)
当股价小于执行价格时：
组合净损益=—Ma*(45-股票市价)+4
根据组合净损益=0 可知，股票市价=41(元)
所以，确保该组合不亏损的股票价格区间为大于或等于41 元、小于或等于49 元。
如果6 个月后的标的股票价格实际上涨20%，即股票价格为48 元，则：
组合净损益=—(48-45)+4=1(元)
(2)看涨期权的股价上行时到期日价值=40*(1+25%)—45=5(元)
2%=上行概率*25%—(1-上行概率)*20%
解得上行概率=0.4889
由于股价下行时到期日价值=0，所以看涨期权价值=(5*0.4889)/(1+2%)=2.40(元)
看跌期权价值=45/(1+2%)+2.40-40=6.52(元) -
第3题：
假设某欧式看涨期权目前股价为4.6元，期权的行权价为4.5元，期限为1年，股价年波动率为0.3，无风险利率为6%，则该看涨期权的价值为（）元。(已知累积正态分布表N(0.42)=0.6628，N(0.12)=0.5478)A、0.96
B、0.54
C、0.66
D、0.72答案：D解析：
@## -
第4题：
标的资产为不支付红利的股票，当前价格为 30 元，已知 1 年后该股票价格或为 37.5 元，或为 25 元，风险中性概率为 0.6。假设无风险利率为 8%，连续复利，计算对应 1 年期，执行价格为 25 元的看涨期权理论价格为（ ）元。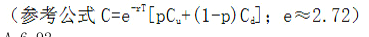
A.6.92
B.7.23
C.6.54
D.7.52答案：A解析：
-
第5题：
某无股息股票看涨期权期限为2个月，执行价格20元，股票当前价格为22元，假设无风险利率为6%，按连续复利计算，则该期权的价格下限为（）元。
- A、1.80
- B、2.00
- C、2.20
- D、2.60
正确答案:C -
第6题：
假设某股票现在价格为40元，1个月后股价变为42元或38元，无风险年利率为8%（连续复利）。试为施行价格为39元、期限为1个月的欧式看涨期权定价。
正确答案:设价格上升到42元的概率为P，则下降到38元的概率为1□P，根据风险中性定价法有
[42P+38（1-P）]e^（-8%*1/12）=40 ；即P=0.5669
设该期权价值为f，则有f=[（42-38）P-0（1-P）]e^（-8%*1/12）=1.69元 -
第7题：
当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年的看跌期权的价格所用的风险中性概率为（）
- A、0.59
- B、0.65
- C、0.75
- D、0.5
正确答案:A -
第8题：
单选题某无股息股票看涨期权期限为2个月，执行价格20元，股票当前价格为22元，假设无风险利率为6%，按连续复利计算，则该期权的价格下限为（）元。A1.80
B2.00
C2.20
D2.60
正确答案： B解析： 暂无解析 -
第9题：
单选题假设某欧式看涨期权目前股价为4.6元，期权的行权价为4.5元，期限为1年，股价年波动率为0.3，无风险利率为6%，则该看涨期权的价值为()元。(已知累积正态分布表N(0.42)=0.6628，N(0.12)=0.5478)A0.96
B0.54
C0.66
D0.72
正确答案： C解析： 暂无解析 -
第10题：
单选题欧式看涨期权和欧式看跌期权的执行价格均为19元，12个月后到期，若无风险年利率为6％，股票的现行价格为18元，看跌期权的价格为0．5元，则看涨期权的价格为（）元。A0.5
B0.58
C1
D1.5
正确答案： B解析： 利用看涨期权——看跌期权平价定理，18+0．5=C+19／（1+6％），则C=0．58（元）。 -
第11题：
单选题当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年的看跌期权的价格所用的风险中性概率为（）A0.59
B0.65
C0.75
D0.5
正确答案： A解析： 暂无解析 -
第12题：
单选题当前股价为15元，一年后股价为20元或10元，无风险利率为6%，计算剩余期限为1年的看跌期权的价格所用的无风险中性概率为()。A0.59
B0.65
C0.75
D0.5
正确答案： B解析： 根据已知条件，可得u=20/15=4/3，d =10/15= 2/3，代入计算公式，可得看跌期权的价格所用的无风险中性概率为0.59。 6.[单选题]按照行权期限的不同，期权可以分为()。 选项: A.欧式期权和美式期权 B.商品期权和金融期权 C.看涨期权和看跌期权 D.现货期权和期货期权 答案:A 分数:1.0 分类:金融类/证券从业及专项/发布证券研究报告业务(证券分析师)/第十章 衍生产品/第三节 期权估值 标签: 按照行权期限的不同，期权的划分 解析:按照买方执行期权时对行权时间规定的不同，可以将期权分为美式期权和欧式期权。美式期权是指期权买方在期权有效期内的任何交易日都可以行使权利的期权到期日行使权利的期权。 -
第13题：
D公司股票当前市价为每股50元。有一种以该股票为标的资产的看涨期权，执行价格为52.08元，到期时间是6个月。6个月以内公司不会派发股利，6个月以后股价有2种变动的可能：上升到66.67元或者下降到37.5元。国库券年报酬为4%。
要求：利用风险中性原理，计算股价上行时的期权价值、上行概率以及该看涨期权的价值。答案：解析：（1）股价上行的期权价值＝66.67-52.08＝14.59（元）
股价下行时的期权价值＝0
（2）假设上行概率为w
4%/2＝w×[（66.67-50）/50]+（1-w）×[（37.5-50）/50]
2020新版教材习题陆续更新，瑞牛题库考试软件，www.niutk.com
则：w＝0.4628
（3）期权价值＝（0.4628×14.59）/（1+2%）＝6.62（元） -
第14题：
某股票当前价格是100元，一年之后预期股价上涨10%或下跌10%，市场无风险利率为8%，运用二又树模型计算执行价格为105元，期限为一年的欧式看涨期权的价值。答案：解析：
-
第15题：
当前股价为15元，一年后股价为20元或10元，无风险利率为6%，计算剩余期限为1年的看跌期权的价格所用的无风险中性概率为（）。（参考公式
A、0.59
B、0.65
C、0.75
D、0.5答案：A解析：根据已知条件，可得u=20/15=4/3；d=10/15=2/3，代入计算公式，可得：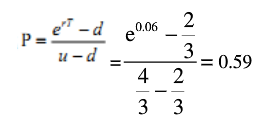
-
第16题：
当前股价为l5元，一年后股价为20元或l0元，无风险利率为6％，计算剩余期限为1年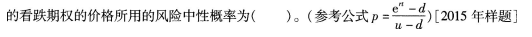
A.0．59
B.0．65
C.0．75
D.0．5答案：A解析：根据已知条件，可得／Z=20／15=4／3；d=10／15=2／3。代入计算公式，可得
-
第17题：
甲公司股票当前每股市价40元，6个月以后股价有两种可能：上升25％或下降20％，市场上有两种以该股票为标的资产的期权：看涨期权和看跌期权。每份看涨期权可买入1股股票，每份看跌期权可卖出1股股票，两种期权执行价格均为45元，到期时间均为6个月，期权到期前，甲公司不派发现金股利，半年无风险报酬率为2％。利用风险中性原理，计算看涨期权的股价上行时到期日价值、上行概率及期权价值，利用看涨期权一看跌期权平价定理，计算看跌期权的期权价值。
正确答案: 看涨期权的股价上行时到期日价值=40×（1+25％）-45=5（元）2％=上行概率×25％+（1-上行概率）×（-20％）
即：2％=上行概率×25％-20％+上行概率×20％
则：上行概率=0.4889
由于股价下行时到期日价值=0
所以，看涨期权价值=（5×0.4889+0.5111×0）／（1+2％）=2.4（元）
看跌期权价值=45／（1+2％）+2.4-40=6.52（元） -
第18题：
假设股票现在的价格为100元，不支付股利，以3个月为一期，3个月内股价可能上涨到原来的1.2倍，也可能下降到原来的0.8倍，无风险利率为12%（连续复利）。试求6个月后到期的执行价格为110元的美式看跌期权的价格。
正确答案:F=e^-0.12×0.25（5.7587×e^0.12×0.25-0.8/1.2-0.8+30×1.2-e^0.12×0.25/1.2-0.8）=15.56（元） -
第19题：
ABC公司的股票目前的股价为10元，有1股以该股票为标的资产的欧式看涨期权，执行价格为10元，期权价格为2元，到期时间为6个月。假设年无风险利率为4％，计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格；
正确答案:看跌期权价格=看涨期权价格-标的资产价格+执行价格现值=2-10+10／(1+2％)=1．80(元) -
第20题：
问答题假设某股票现在价格为40元，1个月后股价变为42元或38元，无风险年利率为8%（连续复利）。试为施行价格为39元、期限为1个月的欧式看涨期权定价。正确答案： 设价格上升到42元的概率为P，则下降到38元的概率为1□P，根据风险中性定价法有
[42P+38（1-P）]e^（-8%*1/12）=40 ；即P=0.5669
设该期权价值为f，则有f=[（42-38）P-0（1-P）]e^（-8%*1/12）=1.69元解析： 暂无解析 -
第21题：
单选题欧式看涨期权和欧式看跌期权的执行价格均为19元，l2个月后到期，若无风险年利率为6％，股票的现行价格为l8元，看跌期权的价格为0.5元，则看涨期权的价格为（）。A0.5元
B0.58元
C1元
D1.5元
正确答案： C解析： 暂无解析 -
第22题：
单选题某股票的现行价格为20元，以该股票为标的资产的欧式看涨期权和欧式看跌期权的执行价格均为24．96元，都在6个月后到期。年无风险利率为8％，如果看涨期权的价格为l0元，看跌期权的价格为（）元。A6.89
B13.1l
C14
D6
正确答案： B解析： 根据看涨期权-看跌期权平价定理得：20+看跌期权价格=10+24．96／（1+4％），所以看跌期权价格=10+24．96÷1．04-20=14（元）。 -
第23题：
问答题ABC公司的股票目前的股价为10元，有1股以该股票为标的资产的欧式看涨期权，执行价格为10元，期权价格为2元，到期时间为6个月。假设年无风险利率为4％，计算1股以该股票为标的资产、执行价格为10元、到期时间为6个月的欧式看跌期权的价格；正确答案： 看跌期权价格=看涨期权价格-标的资产价格+执行价格现值=2-10+10／(1+2％)=1．80(元)解析： 暂无解析 -
第24题：
问答题假设A公司目前的股票价格为20元/股，以该股票为标的资产的看涨期权到期时间为6个月，执行价格为24元，预计半年后股价有两种可能，上升30%或者下降23%，半年的无风险利率为4%。要求： （1）用复制原理计算该看涨期权的价值； （2）用风险中性原理计算该看涨期权的价值； （3）如果该看涨期权的现行价格为2.5元，请根据套利原理，构建一个投资组合进行套利。正确答案：
(1)复制原理:
上行股价=20×(1+30%)=26(元)
下行股价=20×(1—23%)=15.4(元)
套期保值比率H=[(26-24)-0]/(26-15.4)=0.1887
借款数额=(0.1887×15.4-0)/(1+4%)=2.7942(元)
购买股票支出=0.1887×20=3.774(元)
期权价值=3.774-2.7942=0.98(元)
(2)风险中性原理:
4%=上行概率×30%+(1-上行概率)×(-23%)
求得:上行概率=0.5094下行概率=1-0.5094=0.4906
期权到期时价值=0.5094×(26-24)+0.4906×0=1.0188(元)
期权价值=1.0188/(1十4%)=0.98(元)
(3)由于期权价格高于期权价值,因此,套利过程如下:买人0.1887股股票,借入款项2.7942元,同时卖出1股看涨期权,收到2.5元,结果获利=2.5+2.7942-0.1887×20=1.52(元)解析： 暂无解析