单选题甲、乙两人下棋,甲胜的概率为40%,甲不输的概率为90%,则甲、乙两人下成和棋的概率为( ).A 60%B 30%C 10%D 50%
题目
单选题
甲、乙两人下棋,甲胜的概率为40%,甲不输的概率为90%,则甲、乙两人下成和棋的概率为( ).
A
60%
B
30%
C
10%
D
50%
相似考题
更多“甲、乙两人下棋,甲胜的概率为40%,甲不输的概率为90%,则甲、乙两人下成和棋的概率为( ).”相关问题
-
第1题:
甲和乙两个人进行射箭比赛,各射2支箭。已知甲每次射中的概率是60%,乙每次射中的概率是40%,若射中得1分,不中得0分,则两人得分相同的概率( )。A.小于10%
B.在20%到30%之间
C.在30%到40%之间
D.在50%到60%之间答案:C解析:得分相同,可能都是0分,都得1分,都得2分。
(1)都是 0 分的概率为:P0=(1-0.6)2 X (1-0. 4)2 =0. 0576。
(2)都得 1 分的概率为:P1=2X0. 6X(1-0. 6)X2X0. 4X(1-0. 4)=0. 2304。
(3)都得 2 分的概率为:P2=0. 62 X0. 42=0. 0576。
所以得分相同的概率为 0.0576+0. 2304 + 0. 0576 = 0. 3456,即34.56%。 -
第2题:
甲、乙两人各自独立射击1次,甲射中目标的概率为0.8,乙射中目标的概率为0.9,则至少有一人射中目标的概率为()A.0.98
B.0.9
C.0.8
D.0.72答案:A解析:【考情点拨】本题考查了概率的知识点.
-
第3题:
甲、乙两人从1,2,…,15中各取一个数,设甲取到的数是5的倍数,求甲数大于乙数的概率.答案:解析:
-
第4题:
甲和乙进行9局5胜制的台球比赛,结果甲只用了7局就战胜了乙,问在两人所有可能的比赛结果中,甲至少连胜三局的概率为:A.4/5
B.6/7
C.13/15
D.16/21答案:A解析:第一步,本题考查概率问题,属于其他概率问题。
第二步,甲用7局战胜,则甲必须在第7局取胜,且在前6局中有4局取胜,总情况为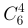 =15(种)。满足至少连胜三局条件的情况比较复杂,以逆向思维解题,考虑不满足连胜三局的情况,枚举得以下3种情况:
=15(种)。满足至少连胜三局条件的情况比较复杂,以逆向思维解题,考虑不满足连胜三局的情况,枚举得以下3种情况:

第三步,满足至少连胜三局的情况数为15-3=12,则甲至少连胜三局的概率为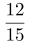 =
=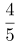 。
。
因此,选择A选项。 -
第5题:
甲乙比赛围棋,约定先胜2局者胜,已知每局甲胜概率0.6,乙为0.4,若第一局乙胜,则甲赢得比赛概率为A.0.144
B.0.288
C.0.36
D.0.4
E.0.6答案:C解析: -
第6题:
甲、乙两人进行五子棋比赛,必须要经过A、B、C三场比赛的角逐,甲对乙每局获胜的概率 为60%,乙对甲每局获胜的概率为40%,则甲胜出的可能性为( )。
A.小于15%
B.介于15%--40%内
C.介于40%--60%内
D.大于60%答案:D解析:本题考查了分步计数原理和分类计数原理。甲胜出的可能情况有两种: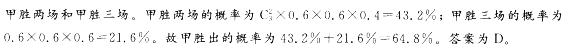
-
第7题:
已知甲、乙两人击中目标的概率分别为0.7、0.8(两人互不影响),两人均射击一次,则目标被击中的概率为()。
- A、0.8
- B、0.94
- C、0.7
- D、0.72
正确答案:B -
第8题:
已知甲、乙两人击中目标的概率分别为0.9、0.8(两人互不影响),两人均射击一次,则两人中只有一人击中目标的概率为()。
- A、0.8
- B、0.18
- C、0.74
- D、0.26
正确答案:D -
第9题:
甲和乙参加乒乓球比赛,五局三胜,两人水平相当,赢球概率都是 50%。 如果甲已经赢 了前两局,那么甲最后获胜的概率是:
A.50%
B.75%
C.87.5%
D.90%答案:C解析:考虑对立面:乙获胜。甲已经连胜2局,乙获胜则必须连胜3局,概率为0.5×0.5×0.5=0.125。则甲最后获胜的概率是1-0.125=0.875。 -
第10题:
甲、乙两人独立地向同一目标射击,甲、乙两人击中目标的概率分别为0.8,
0.5,两人各射击1次,求至少有1人击中目标的概率.答案:解析:
-
第11题:
甲、乙两人独立对同一目标进行射击,命中目标概率分别为60%和50%.
(1)甲、乙两人同时向目标射击,求目标被命中的概率;
(2)甲、乙两人任选一人,由此入射击,目标被击中,求是甲击中的概率.答案:解析:【解】(1)设A={甲击中目标},B={乙击中目标},C={击中目标},则C=A+B,
P(C)=P(A+B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B)
=0.6+0.5-0.6×0.5=0.8.
(2)设A1={选中甲},A2={选中乙},B={目标被击中},则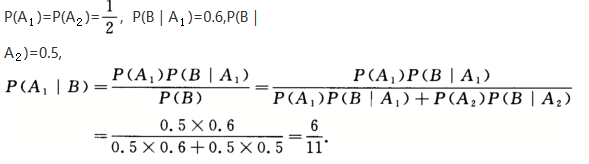
-
第12题:
某车间有甲.乙两台机床,已知甲机床停机的概率为0.06,乙机床停机的概率为0.07,甲.乙两车床同时停机的概率是()A.0.13
B.0.0042
C.0.03
D.0.04答案:B解析: -
第13题:
甲和乙进行5局3胜的乒乓球比赛,甲每局获胜的概率是乙每局获胜概率的1.5倍。问以下哪种情况发生的概率最大?A.比赛在3局内结束
B.乙连胜3局获胜
C.甲获胜且两人均无连胜
D.乙用4局获胜答案:A解析:第一步,本题考查概率问题。
第二步,根据甲获胜的概率是乙获胜概率的1.5倍,令乙获胜的概率为2x,则甲为3x,又甲获胜的概率和乙获胜的概率总和为1,可列式2x+3x=1,解得x=20%,则乙获胜的概率为40%,甲获胜的概率为60%。
第三步,选项信息充分,采用代入排除法解题。
代入A选项,比赛在3局内结束,则情况为甲前3局获胜或乙前3局获胜,概率为
(60%)^3+(40%)^3;
代入B选项,乙连胜3局获胜,情况有三种:乙前3局连胜、乙第一局输后面的三局连胜、乙前两局输后面的三局连胜,概率为(40%)^3+60%×(40%)^3+60%×60%×(40%)3;
代入C选项,甲获胜且两人均无连胜,则情况只有一种:甲胜乙胜甲胜乙胜甲胜,概率为60%×40%×60%×40%×60%;
代入D选项,乙用4局获胜,则情况为前3局乙胜2局,最后一局为乙胜,概率为;
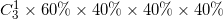
AB选项计算方式接近,优先进行比较:
(60%)^3+(40%)^3>60%×(40%)^3+60%×60%×(40%)3,排除B选项。
CD选项计算方式接近,优先进行比较。D选项数据>C选项数据,排除C选项。
AD比较,(60%)^3+(40%)^3>
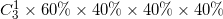
-
第14题:
甲、乙两人随意入住两间房,则甲、乙两人住同一间房的概率是()。
- A、1/4
- B、1/2
- C、2/3
- D、1/3
正确答案:B -
第15题:
甲乙两人下棋,甲胜的概率为0.6,乙胜的概率为0.4,设A为甲胜,B为乙胜,则甲胜乙输的概率为()
- A、0.6∞0.6
- B、0.6-0.6∞0.4
- C、0.6-0.4
- D、0.6
正确答案:D -
第16题:
单选题甲、乙两人轮流投篮,每人每次投一球。约定甲先投且先投中者获胜,一直到有人获胜或每人都已投球3次时投篮结束。设甲每次投篮投中的概率为1/3,乙每次投篮投中的概率为1/2,且各次投篮互不影响。则投篮结束时乙只投了两个球的概率为:A1/27
B1/9
C4/27
D13/27
正确答案: B解析: 暂无解析
