单选题下列等式中是一阶差分方程的是（　　）。A Δ2yt＝yt＋2－2yt＋1＋ytB 3Δyt＋3yt＝t－2C 3Δyt＝2yt－tD yt＋1（1－2t）＋yt－1＝3t

题目
单选题
下列等式中是一阶差分方程的是（　　）。
A

Δ2yt＝yt＋2－2yt＋1＋yt

B

3Δyt＋3yt＝t－2

C

3Δyt＝2yt－t

D

yt＋1（1－2t）＋yt－1＝3t

相似考题

1.乘数==(本期投资It－上期投资It–1)／(本期产出Yt－上期产出Yt－1)()此题为判断题(对，错)。

2.微分方程数值解法的基本思想是：通过某种离散化手段，将微分方程转化为()来求解。A、差分方程B、代数方程C、一阶方程D、以上都不对

3.在0、-4、3、-3、1/5、-5、4、-10中，______是方程x+4=0的解；______是不等式x+4≥0的解；______是不等式x+4＜0的解。）比较a与2a的大小。

4.关于差分法内容下列叙述正确的是()。A、将微分用有限差分来代替。B、将导数用有限差商来代替。C、将微分方程用差分方程(代数方程)代替。D、将微分方程用变分方程代替。

更多“单选题下列等式中是一阶差分方程的是（　　）。A Δ2yt＝yt＋2－2yt＋1＋ytB 3Δyt＋3yt＝t－2C 3Δyt＝2yt－tD yt＋1（1－2t）＋yt－1＝3t”相关问题

  • 第1题：

    解释模型可以表示为：Pt=f(xt，yt，zt)；而预测模型则是Pt=f(xt-1，yt-1，zt-1)。（ ）


    正确答案：A
    从影响因素与价格间的时间角度看，模型可以分为两类：一类是解释模型，另一类则是预测模型，两者有着本质上的区别。比如，在变量下面以下标t、t-1的形式来表示变量发生的时间，则解释模型可以表示为：Pt=f(xt，yt，zt)；而预测模型则是：Pt=f(xt-1，yt-1，zt-1)。

  • 第2题：

    下列一阶微分方程中，哪一个是一阶线性方程？


    答案：A
    解析：
    提示：把一阶阶段方程化为x'+p（y）x=Q（y）的形式。

  • 第3题：

    对于模型：Yt=β1β2Xt+μt。如果用变量的一阶差分估计该模型，则意味着采用了何种自相关形式？


    正确答案: 若题目要求用变量的一次差分估计该模型，即采用了如下形式：Yt-Yt-1=β2（Xt-Xt-1）+（μt-μt-1）或ΔYt=β2ΔXt+εt
    这时意味着μt=μt-1+εt，即随机扰动项是自相关系数为1的一阶自相关形式。

  • 第4题：

    对于典型一阶系统，以下说法正确的是（）。

    • A、单位阶跃响应是一个按指数规律上升的曲线
    • B、时间常数T越大，上升过程越慢
    • C、初始条件为零时的单位阶跃响应在t经历3T时，达到稳态值的95%
    • D、对应的微分方程数学模型为一阶线性常微分方程

    正确答案:A,B,C,D

  • 第5题：

    运用三次曲线方程拟合趋势延伸法预测模型时，时间序列的（）必须为常数。

    • A、一阶差分
    • B、二阶差分
    • C、三阶差分
    • D、一阶差分的对数

    正确答案:D

  • 第6题：

    信号 f（5-3t） 是（）

    • A、f（3t）右移5
    • B、f（3t）左移5
    • C、f（-3t）左移5
    • D、f（-3t）右移5

    正确答案:D

  • 第7题：

    填空题
    已知函数yt＝t（t－1）/2＋C是方程yt＋1－yt＝f（t）的解，则f（t）＝____。

    正确答案： t
    解析：
    yt＋1－yt＝（t＋1）t/2－t（t－1）/2＝t＝f（t）

  • 第8题：

    填空题
    差分方程yt＋1－yt＝t2t的通解为____。

    正确答案： yt=c+(t-2)2t
    解析：
    原差分方程对应的齐次方程yt＋1－yt＝0的通解为y(＿)t＝c（1t）＝c。设y(＿)t＝（At＋B）2t，则yt＋1－yt＝[A（t＋1）＋B]2t＋1－（At＋B）2t＝2t（2At＋2A＋2B－At－B）＝2t（At＋2A＋B）＝t·2t。解得A＝1，B＝－2。故y(＿)t＝（t－2）2t，则yt＝c＋（t－2）2t。

  • 第9题：

    单选题
    下列等式中，不是差分方程的是（　　）。
    A

    2Δyt－yt＝2

    B

    3Δyt＋3yt＝t

    C

    Δ2yt＝0

    D

    yt－yt－2＝et


    正确答案： D
    解析：
    B项中，由于3Δyt＋3yt＝3（yt＋1－yt）＋3yt＝3yt＋1，故原等式为3yt＋1＝t，它不是差分方程。

  • 第10题：

    单选题
    信号f（5-3t）是（）
    A

    f（3t）右移5

    B

    f（3t）左移

    C

    f（－3t）左移5

    D

    f（－3t）右移


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    运用三次曲线方程拟合趋势延伸法预测模型时，时间序列的（）必须为常数。
    A

    一阶差分

    B

    二阶差分

    C

    三阶差分

    D

    一阶差分的对数


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    不稳态导热采用有限差分方法求解温度场，关于差分方程，下列说法错误的是（　　）。
    A

    显式差分格式是温度对时间的一阶导数采用向前差分获得，具有稳定性条件

    B

    隐式差分格式是温度对时间的一阶导数采用向后差分获得，没有稳定性条件

    C

    显式差分格式中温度对位置的二阶导数采用中心差分格式获得

    D

    隐式差分格式是温度对位置的二阶导数采用向后差分获得


    正确答案： A
    解析：
    AC两项，显式差分格式中，温度是对时间的一阶导数，采用向前差分；温度是对位置的二阶导数，采用中心差分格式，具有稳定性条件。BD两项，隐式差分格式中，温度是对时间的一阶导数，采用向后差分；温度是对位置的二阶导数，采用中心差分格式，没有稳定性条件。

  • 第13题：

    已知一阶微分方程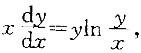问该方程的通解是下列函数中的哪个？


    答案：B
    解析：
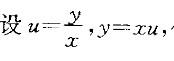    提示:方程是一阶齐次方程，化为可分离变量方程求通解。

  • 第14题：

    下列等式中是一阶查分方程的是（ ）.《》（ ）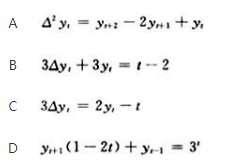


    答案：C
    解析：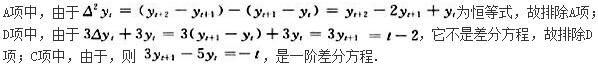

  • 第15题：

    信号f（5-3t）是（）

    • A、f（3t）右移5
    • B、f（3t）左移
    • C、f（－3t）左移5
    • D、f（－3t）右移

    正确答案:D

  • 第16题：

    对于模型：Yt=β1β2Xt+μt。在用一阶差分估计时，如果包含一个截距项，其含义是什么？


    正确答案: 在一阶差分形式中出现有截距项，意味着在原始模型中有一个关于时间的趋势项，截距项事实上就是趋势变量的系数，即原模型应为
    Yt=β0+β1t+β2Xt+μt

  • 第17题：

    信号f（3t+6）是（）运算的结果。

    • A、f（3t）右移2
    • B、f（3t）左移2
    • C、f（3t）左移6
    • D、f（3t）右移6

    正确答案:B

  • 第18题：

    单选题
    差分方程yt＋1－yt＝t2t的通解为（　　）。
    A

    yt＝c＋（t2＋2）2

    B

    yt＝c＋（t2－2）2t

    C

    yt＝c＋（t＋2）2t

    D

    yt＝c＋（t－2）2t


    正确答案： C
    解析：
    原差分方程对应的齐次方程yt＋1－yt＝0的通解为y(＿)t＝c（1t）＝c。设y(＿)t＝（At＋B）2t，则yt＋1－yt＝[A（t＋1）＋B]2t＋1－（At＋B）2t＝2t（2At＋2A＋2B－At－B）＝2t（At＋2A＋B）＝t·2t。解得A＝1，B＝－2。故y(＿)t＝（t－2）2t，yt＝c＋（t－2）2t。

  • 第19题：

    填空题
    差分方程2yt＋1＋10yt－5t＝0的通解为____。

    正确答案： yt=c(-5)t+(5/12)(t-1/6)
    解析：
    原差分方程为2yt＋1＋10yt－5t＝0，即yt＋1＋5yt＝5t/2。对应齐次方程的通解为y(＿)t＝c（－5）t，假设y(＿)t＝At＋B为原方程的特解，则将其代入原方程，解得A＝5/12，B＝－5/72。故所求通解为yt＝c（－5）t＋（5/12）（t－1/6）。

  • 第20题：

    填空题
    设yt＝et，则Δ2yt＝____。

    正确答案： et(e-1)2
    解析：
    Δ2yt＝（yt＋2－yt＋1）－（yt＋1－yt）＝yt＋2－2yt＋1＋yt＝et＋2－2et＋1＋et＝et（e2－2e＋1）＝et（e－1）2

  • 第21题：

    单选题
    方程yt－3yt－1＝－4的一般解为（　　）。
    A

    yt＝C3t＋2

    B

    yt＝3t－2

    C

    yt＝C（－3）t－2

    D

    yt＝C3t－2


    正确答案： D
    解析：
    B项中，没有自由常数，排除B项；C项中，由于原方程对应齐次方程的通解为y(＿)＝C（－a）t＝C3t，故排除C项；D项中，－2－3×（－2）＝4≠－4，故排除D项。

  • 第22题：

    单选题
    已知函数yt＝t（t－1）/2＋C是方程yt＋1－yt＝f（t）的解，则f（t）＝（　　）。
    A

    t－1

    B

    t－2

    C

    t

    D

    2－t


    正确答案： A
    解析：
    yt＋1－yt＝（t＋1）t/2－t（t－1）/2＝t＝f（t）。

  • 第23题：

    单选题
    以函数yt＝A2t＋8为通解的差分方程是（　　）。
    A

    yt＋2－3yt＋1＋2yt＝0

    B

    yt－3yt－1＋2yt－2＝0

    C

    yt＋1－2yt＝－8

    D

    yt＋1－2yt＝8


    正确答案： D
    解析：
    A项中，由于该差分方程为二阶常系数差分方程，故其通解中应含有两个任意常数，故排除A项；同理可知，yt＝A2t＋8也不是B项二阶差分方程的通解；将yt＝A2t＋8代入C选项中，可知，等式两边相等，且C项是一阶常系数差分方程。故yt＝A2t＋8是C中差分方程的通解。

相关内容