单选题设有向量组α(→)1＝（1，－1，1，0），α(→)2＝（1，2，－1，0），α(→)3＝（0，1，1，1），α(→)4＝（2，2，1，1），则以下命题正确的是（ ）。A α(→)1线性相关B α(→)1，α(→)2线性相关C α(→)1，α(→)2，α(→)3线性相关D α(→)1，α(→)2，α(→)3，α(→)4线性相关
题目
单选题
设有向量组α(→)1＝（1，－1，1，0），α(→)2＝（1，2，－1，0），α(→)3＝（0，1，1，1），α(→)4＝（2，2，1，1），则以下命题正确的是（ ）。
A
α1线性相关
B
α1，α2线性相关
C
α1，α2，α3线性相关
D
α1，α2，α3，α4线性相关
相似考题
更多“设有向量组α(→)1＝（1，－1，1，0），α(→)2＝（1，2，－1，0），α(→)3＝（0，1，1，1），α(→)4”相关问题
-
第1题：
向量组a₁=(1 ,2,3),a₂=(1,0,0),a₃=(1,1,0)线性___________.
参考答案无关
-
第2题：
与向量(1，3，1)和(1，0，2)同时垂直的向量是( )。A.(3，-1，0)
B.(6，-1，-3)
C.(4，0，-2)
D.(1，0，1)答案：B解析：
-
第3题：
设向量组A：a1=(1，-1，0)，a2=(2，1，t)，a3=(0，1，1)线性相关，则t等于( ).A.1
B.2
C.3
D.0答案：C解析：
-
第4题：
设直线的方程为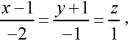
则直线：
(A)过点(1,-1,0)，方向向量为2i + j-k
(B)过点(1,-1,0)，方向向量为2i - j + k
(C)过点(-1,1,0)，方向向量为-2i - j + k
(D)过点(-1,1,0)，方向向量为2i + j - k答案：A解析：设直线L过点M0（x0，y0，z0），它的一个方向向量为s=(m,n,p),则直线L的方程为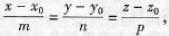
此方程称为直线的对称式方程， 如设参数t如下：
此方程组称为直线的参数式方程。 -
第5题：
利用施密特正交化方法把向量组a1=(0，1，1)′,a2=(1,1,0)′,a3=(1,0,1)′正交化答案：解析：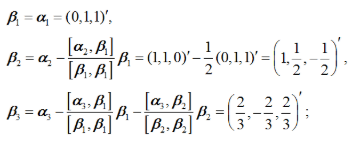
-
第6题：
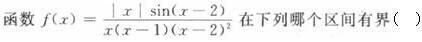A.（-1，0）
B.（0，1）
C.（1，2）
D.（2，3）答案：A解析：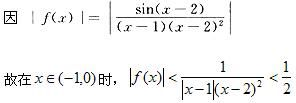
-
第7题：
A=[1，2；3，4]；B=[1，0；0，1]； A*B=（）， A.*B=（）
正确答案:[1 2；3 4]；[1 0；0 4] -
第8题：
设向量组A：α1=（1，-1，0），α2=（2，1，t），α3=（0，1，1）线性相关，则t等于（）。
- A、1
- B、2
- C、3
- D、0
正确答案:C -
第9题：
单选题设有向量组α(→)1＝（1，－1，1，0），α(→)2＝（1，2，－1，0），α(→)3＝（0，1，1，1），α(→)4＝（2，2，1，1），则以下命题正确的是（ ）。Aα1线性相关
Bα1，α2线性相关
Cα1，α2，α3线性相关
Dα1，α2，α3，α4线性相关
正确答案： D解析：
A项，因α1≠0，故α1线性无关；
B项，因α1，α2坐标不成比例，故α1，α2线性无关；
C项，由r（α1，α2，α3）＝3，故α1，α2，α3线性无关；
D项，因r（α1，α2，α3，α4）＝3，故α1，α2，α3，α4线性相关。 -
第10题：
单选题设有向量组α1=（6，λ+1，7），α2=（λ，2，2），α3=（λ，l，0）线性相关，则（ ）.Aλ=1或λ=4
Bλ=2或λ=4
Cλ=3或λ=4
Dλ=-3/2或λ=4
正确答案： B解析： 暂无解析 -
第11题：
单选题设α(→)＝（1，0，－1，2），β(→)＝（0，1，0，2），则r（α(→)Tβ(→)）＝（ ）。A1
B2
C3
D4
正确答案： A解析：
r（αTβ）≤min[r（αT），r（β）]＝1，又αTβ≠0，故r（αTβ）＞0，知r（αTβ）＝1。 -
第12题：
填空题A=[1，2；3，4]；B=[1，0；0，1]； A*B=（）， A.*B=（）正确答案： [1 2,3 4],[1 0,0 4]解析： 暂无解析 -
第13题：
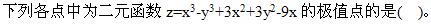A.(1，0)
B.(1，2)
C.(1，1)
D.(-3，0)答案：A解析： -
第14题：
A.过点(-1，2，-3)，方向向量为i+2j-3k
B.过点(-1，2，-3)，方向向量为-i-2j+3k
C.过点(1，2，-3)，方向向量为i-2j+3k
D.过点(1，-2，3)，方向向量为-i-2j+3k答案：D解析：
-
第15题：
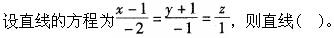A.过点(1，-1，0)，方向向量为2i+j-k
B.过点(1，-1，0)，方向向量为2i-j+k
C.过点(-1，1，0)，方向向量为-2i-j+k
D.过点(-1，1，0)，方向向量为2i+j-k答案：A解析： -
第16题：
利用施密特正交化方法把向量组a1=(1,0,-1,1), a2=(1,-1,0,1), a3=(-1,1,1,0)正交化答案：解析：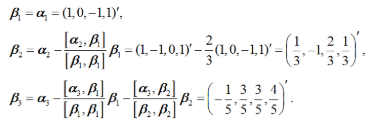
-
第17题：
设α1=(1，2，-1，0)^T，α2=(1，1，0，2)^T，α3=(2，1，1，α)^T.若由α1，α2，α3生成的向量空间的维数为2，则α=________.答案：1、6.解析：本题考查向量空间及其维数的概念，因为α1，α2，α3所生成的向量空间是2维，亦即向量组的秩r(α1，α2，α3)=2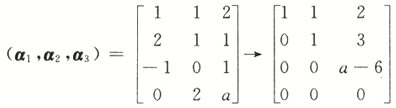
由秩为2，知α=6. -
第18题：
A.（1，0，0，1/2）
B.（1，0，-1，1/2）
C.（1，1，0，-1/2）
D.（2，1，0，-1/2）答案：A解析：
-
第19题：
已知向量组α1=（3，2，-5）T，α2=（3，-1，3）T，，α4=（6，-2，6）T，则该向量组的一个极大无关组是（）。
- A、α2，α4
- B、α3，α4
- C、α1，α2
- D、α2，α3
正确答案:C -
第20题：
设有向量组α1=（2，1，4，3）T，α1=（-1，1，-6，6）T，α3=（-1，-2，2，-9）T，α4=（1，1，-2，7）T，α5=（2，4，4，9）T，则向量组α1，α2，α3，α4，α5的秩是（）。
- A、1
- B、2
- C、3
- D、4
正确答案:C -
第21题：
单选题下列向量组中，能作为表示它们所在平面内所有向量的基底的是（ ）．Ae1＝(0，0)，e2＝(1，－2)
Be1＝(－1，2)，e2＝(5，7)
Ce1＝(3，5)，e2＝(6，10)
De1＝(1，2)，e2＝(2，4)
正确答案： A解析：
要作为表示它们所在平面内所有向量的基底，则向量e1和e2为平面内两个不共线的向量．ACD三项，向量e1和e2都为共线向量． -
第22题：
填空题已知向量组（α1，α3），（α1，α3，α4），（α2，α3，）都线性无关，而（α1，α2，α3，α4）线性相关，则向量组（α1，α2，α3，α4）的极大无关组是____.正确答案： (α1,α3,α4)解析：
向量组（α1，α2，α3，α4）线性相关，则其极大线性无关组最多含三个向量，又（α1，α3，α4）线性无关，故知（α1，α3，α4）为其极大线性无关组． -
第23题：
单选题已知向量组（α(→)1，α(→)3），（α(→)1，α(→)3，α(→)4），（α(→)2，α(→)3）都线性无关，而（α(→)1，α(→)2，α(→)3，α(→)4）线性相关，则向量组（α(→)1，α(→)2，α(→)3，α(→)4）的极大无关组是（ ）。A（α1，α2，α3）
B（α1，α2，α4）
C（α1，α3，α4）
D（α2，α3，α4）
正确答案： B解析：
向量组（α1，α2，α3，α4）线性相关，则其极大线性无关组最多含三个向量，又（α1，α3，α4）线性无关，故知（α1，α3，α4）为其极大线性无关组。 -
第24题：
单选题设α(→)＝（1，0，－1，2）T，β(→)＝（0，1，0，2），矩阵A＝α(→)·β(→)，则秩r（A）＝（ ）。A2
B1
C3
D4
正确答案： A解析：
秩r（A）＝r（α·β）≤r（α）＝1，又α·β≠0，可见r（A）≥1。故r（A）＝1。