问答题试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。

题目
问答题
试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。
相似考题

1.若A是____,则A必为方阵。A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵

2.若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()A、A与B相似B、A≠B，但|A-B|=0C、A=BD、A与B不一定相似，但|A|=|B|

3.节点导纳矩阵的特点有()。A、是n×n阶方阵B、是稀疏矩阵C、一般是对称矩阵D、其对角元一般小于非对角元

4.下列结论或等式正确的是()。A.若A，B均为零矩阵，则有A=BB.矩阵乘法满足交换律，则(AB)k=AkBkC.对角矩阵是对称矩阵D.若A≠0，B≠0，则AB≠0

更多“问答题试证若n阶矩阵A满足A2－A＝2E，则A一定相似于对角矩阵。”相关问题

  • 第1题：

    设n阶矩阵A满足（aE-A）(bE-A)=O且a≠6.证明：A可对角化.


    答案：
    解析：
    【证明】由(aE-A)(bE-A)=O，得|aE-A|·|bE-A|=0，则|aE-A|=0或者
    |bE-A|=0.又由(aE-A)(bE-A)=O，得r(aE-A)+r(bE-A)≤n.
    同时r（aE-A）+r(bE-A)≥r［(aE-A)-(bE-A)］=r［（a-b）E］=n，
    所以r(aE-A)+r(bE-A)=n.
    (1)若|aE-A|≠0，则r（aE-A=n，所以r(bE-A)=0，故A=bE.
    (2)若|bE-A|≠0，则r(bE-A)=n，所以r(aE-A)=0，故A=aE.
    (3)若|aE-A|=0且|bE-A|=0，则a，b都是矩阵A的特征值.
    方程组(aE-A)X=0的基础解系含有n-r（aE-A）个线性无关的解向量，即特征值a对应的线性无关的特征向量个数为n-r（aE-A）个；
    方程组(bE-A)X=0的基础解系含有n-r(bE-A)个线性无关的解向量，即特征值b对应的线性无关的特征向量个数为n-r(bE-A)个.
    因为n-r(aE-A)+n-r(bE-A)=n，所以矩阵A有n个线性无关的特征向量，所以A一定可以对角化.

  • 第2题：

    设A为四阶实对称矩阵，且A^2+A=O.若A的秩为3，则A相似于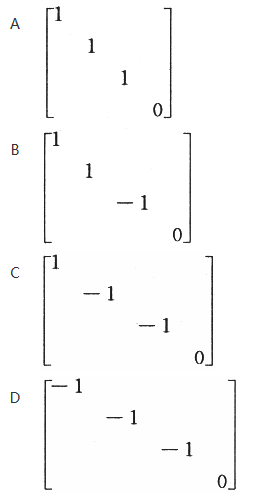


    答案：D
    解析：
    这是一道常见的基础题，由Aα=λα，α≠0知A^nα=λ^nα，那么对于A^2+A=0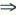(λ^2+λ)α=0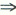λ^2+λ=0所以A的特征值只能是0或-1再由A是实对称必有A～A，而A即是A的特征值，那么由r(A)=3，可知(D)正确

  • 第3题：

    设A为n阶对称矩阵，k为常数.试证kA仍为对称矩阵.


    答案：
    解析：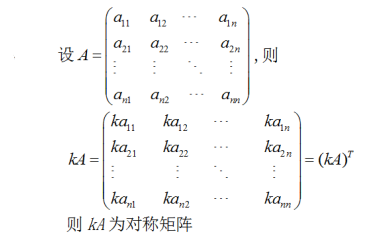

  • 第4题：

    设A，B为n阶矩阵，考虑以下命题：①若A，B为等价矩阵，则A，B的行向量组等价②若行列式.，则A，B为等价矩阵③若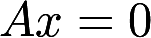与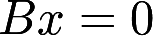都只有零解，则A，B为等价矩阵④若A，B为相似矩阵，则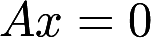与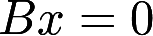的解空间的维数相同以上命题中正确的是（ ）.

    A.①③
    B.②④
    C.②③
    D.③④

    答案：D
    解析：

  • 第5题：

    设A是三阶矩阵，已知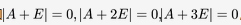 ，B与A相似，则B的相似对角形为


    答案：
    解析：

  • 第6题：

    设3阶矩阵A 满足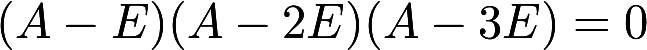 ，证明A可对角化


    答案：
    解析：

  • 第7题：

    与n阶单位矩阵E相似的矩阵是

    A.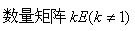
    B.对角矩阵D（主对角元素不为1）
    C.单位矩阵E
    D.任意n阶矩阵A


    答案：C
    解析：

  • 第8题：

    设N阶矩阵A与对角矩阵合同,则A是().

    A.可逆矩阵
    B.实对称矩阵
    C.正定矩阵
    D.正交矩阵

    答案：B
    解析：

  • 第9题：

    设n阶矩阵A与对角矩阵相似,则().

    A.A的n个特征值都是单值
    B.A是可逆矩阵
    C.A存在n个线性无关的特征向量
    D.A一定为n阶实对称矩阵

    答案：C
    解析：
    矩阵A与对角阵相似的充分必要条件是其有n个线性无关的特征向量，A有n个单特征值只是其可对角化的充分而非必要条件，同样A是实对称阵也是其可对角化的充分而非必要条件，A可逆既非其可对角化的充分条件，也非其可对角化的必要条件，选(C).

  • 第10题：

    设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。

    • A、等价
    • B、相似
    • C、合同
    • D、正交

    正确答案:B

  • 第11题：

    单选题
    若具有n个顶点的无向图采用邻接矩阵存储方法，则该邻接矩阵一定为一个（）。
    A

    一般矩阵

    B

    对角矩阵

    C

    对称矩阵

    D

    稀疏矩阵


    正确答案： A
    解析： 暂无解析

  • 第12题：

    填空题
    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。

    正确答案： 上,三角矩阵
    解析： 暂无解析

  • 第13题：

    若矩阵A=,B是三阶非零矩阵,满足AB=O,则t=_______.


    答案：1、1
    解析：
    由AB=0得r(A)+r(B)≤3，因为r(B)≥1，所以r(A)≤2，又因为矩阵A有两行不成比例，所以r(A)≥2，于是r(A)=2.
    　　由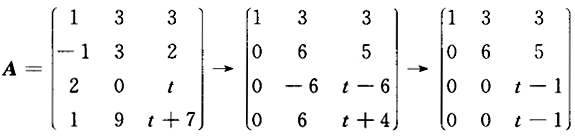得t=1.

  • 第14题：

    下列矩阵中能相似于对角矩阵的是：



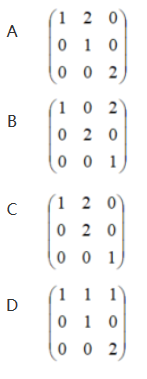    答案：C
    解析：




  • 第15题：

    证明n阶矩阵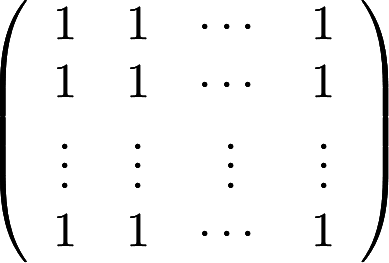与相似


    答案：
    解析：

  • 第16题：

    试证：如果A,B都是n阶正定矩阵，则A+B也是正定的


    答案：
    解析：

  • 第17题：

    设n阶矩阵A 满足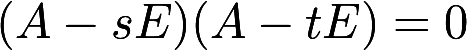，其中s≠t，证明A可对角化


    答案：
    解析：

  • 第18题：

    设A,B为N阶矩阵,且A,B的特征值相同,则().

    A.A,B相似于同一个对角矩阵
    B.存在正交阵Q,使得Q^TAQ=B
    C.r(A)=r(B)
    D.以上都不对

    答案：D
    解析：

  • 第19题：

    设A，B，C均为n阶矩阵，E为n阶单位矩阵，若B=E+AB，C=A+CA，则B-C=



    A.E
    B.-E
    C.A
    D.-A

    答案：A
    解析：

  • 第20题：

    若n阶矩阵A，B有共同的特征值，且各有n个线性无关的特征向量，则（ ）

    A.A与B相似
    B.
    C.A=B
    D.A与B不一定相似，但|A|=|B|


    答案：A
    解析：

  • 第21题：

    若具有n个顶点的无向图采用邻接矩阵存储方法，则该邻接矩阵一定为一个（）。

    • A、一般矩阵
    • B、对角矩阵
    • C、对称矩阵
    • D、稀疏矩阵

    正确答案:C

  • 第22题：

    若一个n阶矩阵A中的元素满足：Aij=Aji（0<=I，j<=n-1）则称A为（）矩阵；若主对角线上方（或下方）的所有元素均为零时，称该矩阵为（）。


    正确答案:上；三角矩阵

  • 第23题：

    单选题
    设A，B都是n阶矩阵，若有可逆矩阵P使得P-1AP=B，则称矩阵A与矩阵B（）。
    A

    等价

    B

    相似

    C

    合同

    D

    正交


    正确答案： D
    解析： 由相似矩阵的定义知B正确。故选B。

相关内容