问答题设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。

题目
问答题
设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。
相似考题

1.A.只能确定一个具有连续偏导数的隐函数z=z（x，y） B.可确定两个具有连续偏导数的隐函数y=y（x，y）和z=z（x，y） C.可确定两个具有连续偏导数的隐函数x=x（x，y）和z=z（x，y） D.可确定两个具有连续偏导数的隐函数x=x（y，z）和y=y（x，z）

2.设函数f(μ，ν)具有二阶连续偏导数，z=f(x，xy)，则=________.

3.设函数z=f(xy，yg(x))，其中函数f具有二阶连续偏导数，函数g(x)可导且在x=1处取得极值g(1)=1.求

4.设z=f(x2-y2)，则dz 等于： A. 2x-2y B. 2xdx-2ydy C. f'(x2-y2)dx D. 2f'(x2-y2)(xdx-ydy)

更多“问答题设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。”相关问题

  • 第1题：

    设函数f(u)具有二阶连续导数，z=f(e^xcosy)满足
    　　
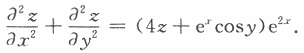
    　　若f(0)=0，f'(0)=0，求f(u)的表达式.


    答案：
    解析：
    【分析】根据已知的关系式，变形得到关于f(u)的微分方程，解微分方程求得f(u).

  • 第2题：

    设有三元方程 ，根据隐函数存在定理，存在点(0,1,1)的一个邻域，在此邻域内该方程

    A.只能确定一个具有连续偏导数的隐函数z=z(x,y)
    B.可确定两个具有连续偏导数的隐函数x=x(y,z)和z=z(x,y)
    C.可确定两个具有连续偏导数的隐函数y=y(x,z)和z=z(x,y)
    D.可确定两个具有连续偏导数的隐函数x=x(y,z)和y=y(x,z)

    答案：D
    解析：

  • 第3题：

    设z=f（x2－y2），则dz 等于：

    A. 2x－2y
    B. 2xdx－2ydy
    C. f’（x2－y2）dx
    D.2f’（x2－y2）（xdx—ydy）

    答案：D
    解析：

  • 第4题：

    设z=f（x2+y2），其中f具有二阶导数，则等于（）．

    • A、2f’（x2+y2）
    • B、4x2f"（x2+y2）
    • C、2’（x2+y2）+4x2f"（x2+y2）
    • D、2xf"（x2+y2）

    正确答案:C

  • 第5题：

    下列结论正确的是（）．

    • A、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
    • B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
    • C、z=（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
    • D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件

    正确答案:D

  • 第6题：

    问答题
    设z＝f（u），而u＝u（x，y）满足u＝y＋xφ（u）。若f和φ有连续导数，u存在偏导数，且xφ′（u）≠1，证明：∂z/∂x＝φ（u）∂z/∂y。

    正确答案：
    原方程u=y+xφ(u),两边分别对x、y求偏导得∂u/∂x=φ(u)+xφ′(u)∂u/∂x,∂u/∂y=1+xφ′(u)∂u/∂y。
    即∂u/∂x=-φ(u)/[xφ′(u)-1],∂u/∂y=-1/[xφ′(u)-1]。
    又∂z/∂x=(df/du)·(∂u/∂x)=(df/du)·[φ(u)/(1-xφ′(u))],∂z/∂y=(df/du)·(∂u/∂y)=(df/du)·[1/(1-xφ′(u))]。
    则∂z/∂x=φ(u)∂z/∂y。
    解析： 暂无解析

  • 第7题：

    单选题
    设f有二阶偏导数，z＝f（xy），则∂2z/∂x∂y等于（　　）。
    A

    yf″＋f′

    B

    xy2f″

    C

    xyf′f″

    D

    f′＋xyf″


    正确答案： B
    解析：
    ∂z/∂x＝yf′，∂2z/∂x∂y＝f′＋yf″·x＝f′＋xyf″。

  • 第8题：

    填空题
    设函数z＝z（x，y）由方程F（x－az，y－bz）＝0所给出，其中F（u，v）任意可微，则a∂z/∂x＋（b∂z/∂y）＝____。

    正确答案： 1
    解析：
    根据偏导数的求解方法可知∂z/∂x＝－Fx′/Fz′＝－F1′/（―aF1′―bF2′），∂z/∂y＝－Fy′/Fz′＝－F2′/（―aF1′―bF2′），故a∂z/∂x＋（b∂z/∂y）＝－（aF1′＋bF2′）/（―aF1′―bF2′）＝1。

  • 第9题：

    单选题
    设u＝f（x＋y，xz）有二阶连续偏导数，则∂2u/∂x∂z＝（　　）。
    A

    f2′＋xf11′＋（x＋z）f12″＋xzf22″

    B

    xf12″＋xzf22″

    C

    f2′＋xf12″＋xzf22″

    D

    xzf22″


    正确答案： B
    解析：
    由u＝f（x＋y，xz），可得∂u/∂x＝f1′·1＋zf2′，则∂2u/（∂x∂z）＝f11″·0＋f12″·x＋f2′＋z（f21″·0＋f22″·x）＝xf12″＋f2′＋xzf22″。

  • 第10题：

    单选题
    （2009）设z=f（x2-y2），则dz等于：（）
    A

    2x-2y

    B

    2xdx-2ydy

    C

    f′（x2-y2）dx

    D

    2f′（x2-y2）（xdx-ydy）


    正确答案： D
    解析： 暂无解析

  • 第11题：

    单选题
    设三元函数xy－zlny＋exz＝1，根据隐函数存在定理，存在点（0，1，1）的一个邻域，在此邻域内该方程（　　）。
    A

    只能确定一个具有连续偏导数的隐函数z＝z（x，y）

    B

    可确定两个具有连续偏导数的隐函数y＝y（x，z）和z＝z（x，y）

    C

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和z＝z（x，y）

    D

    可确定两个具有连续偏导数的隐函数x＝x（y，z）和y＝y（x，z）


    正确答案： C
    解析：
    构造函数F（x，y，z）＝xy－zlny＋exz－1，则Fx′＝y＋zexz，Fy′＝x－（z/y），Fz′＝－lny＋xexz。Fx′（0，1，1）＝2≠0，Fy′（0，1，1）＝－1≠0，Fz′（0，1，1）＝0。
    故根据隐函数的存在定理可知，方程xy－zlny＋exz＝1能确定x是y、z的具有连续偏导数的函数x＝x（y，z）；y是x、z的具有连续偏导数的函数y＝y（x，z）。因为Fz′（0，1，1）＝0不能满足定理成立的条件，故不能确定z是x、y的具有连续偏导数的隐函数z＝z（x，y）。

  • 第12题：

    填空题
    设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。

    正确答案： f2′+xf12″+xyf22″
    解析：
    ∂z/∂x＝f1′＋yf2′，∂2z/（∂x∂y）＝f11″·0＋xf12″＋f2′＋yf22″·x＝xf12″＋f2′＋xyf22″

  • 第13题：

    下列结论正确的是( ).

    A.x=f(x，y)在点(x，y)的偏导数存在是f(x，y)在该点连续的充分条件
    B.z=f(x，y)在点(x，y)连续是f(x，y)的偏导数存在的必要条件
    C.z=f(x，y)在点(x，y)的偏导数存在是f(x，y)在该点可微分的充分条件
    D.z=(x，y)在点(x，y)连续是f(x，y)在该点可微分的必要条件

    答案：D
    解析：
    由z=f(x，y)在点(x，y)可微分的定义知，函数在一点可微分必定函数在该点连续， 故D正确.

  • 第14题：

    设 , 其中f具有二阶连续偏导数, 求


    答案：
    解析：

  • 第15题：

    设z=f(x2-y2)，则dz 等于：

    A. 2x-2y
    B. 2xdx-2ydy
    C. f'(x2-y2)dx
    D. 2f'(x2-y2)(xdx-ydy)

    答案：D
    解析：

  • 第16题：

    下列结论正确的是（）.

    • A、x=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
    • B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
    • C、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
    • D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件

    正确答案:D

  • 第17题：

    单选题
    设z=f（x2+y2），其中f具有二阶导数，则等于（）．
    A

    2f’（x2+y2）

    B

    4x2f（x2+y2）

    C

    2’（x2+y2）+4x2f（x2+y2）

    D

    2xf（x2+y2）


    正确答案： A
    解析： 暂无解析

  • 第18题：

    单选题
    设z＝φ（x2－y2），其中φ有连续导数，则函数z满足（　　）。
    A

    x∂z/∂x＋y∂z/∂y＝0

    B

    x∂z/∂x－y∂z/∂y＝0

    C

    y∂z/∂x＋x∂z/∂y＝0

    D

    y∂z/∂x－x∂z/∂y＝0


    正确答案： B
    解析：
    令u＝x2－y2，则z＝φ（u），∂z/∂x＝φ′（u）·2x＝2xφ′（u），∂z/∂y＝－2yφ′（u），故y∂z/∂x＋x∂z/∂y＝0。

  • 第19题：

    填空题
    设z＝f（xy，x/y）＋g（y/x），其中f、g均可微，则∂z/∂x＝____。

    正确答案： yf1′+f2′/y-yg′/x2
    解析：
    设f1′为函数f（u，v）对第一中间变量的偏导，f2′为函数f（u，v）对第二中间变量的偏导，g′为函数g对x的导数。则∂z/∂x＝∂f（xy，x/y）/∂x＋∂g（y/x）/∂x＝f1′y＋f2′·（1/y）＋g′·（－y/x2）＝f1′y＋f2′/y－yg′/x2。

  • 第20题：

    问答题
    若函数f（x，y，z）恒满足关系式f（tx，ty，tz）＝tkf（x，y，z）就称为k次齐次函数，验证k次齐次函数满足关系式（其中f存在一阶连续偏导数）x∂f/∂x＋y∂f/∂y＋z∂f/∂z＝kf（x，y，z）。

    正确答案：
    为简化计算,可令u=tx,v=ty,w=tz,则f(u,v,w)=tkf(x,y,z),两边对t求导,得x∂f/∂u+y∂f/∂v+z∂f/∂w=ktk-1f(x,y,z),则上式对一切实数t都成立。令t=1,得x∂f/∂x+y∂f/∂y+z∂f/∂z=kf(x,y,z)。
    解析： 暂无解析

  • 第21题：

    单选题
    设z＝yφ（x/y），其中φ（u）具有二阶连续导数，则∂2z/（∂x∂y）等于（　　）。[2017年真题]
    A

    （1/y）φ″（x/y）

    B

    （－x/y2）φ″（x/y）

    C

    1

    D

    φ′（x/y）－（x/y）φ″（x/y）


    正确答案： B
    解析：
    计算得
    ∂z/∂x＝y·φ′（x/y）·（1/y）＝φ′（x/y）
    ∂2z/∂x∂y＝－（x/y2）φ″（x/y）

  • 第22题：

    单选题
    设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝（　　）。
    A

    f2′＋f12″＋xyf22″

    B

    f2′＋f12″＋xf22″

    C

    f2′＋xyf12″＋xyf22″

    D

    f2′＋xf12″＋xyf22″


    正确答案： D
    解析：
    ∂z/∂x＝f1′＋yf2′，∂2z/（∂x∂y）＝f11″·0＋xf12″＋f2′＋yf22″·x＝xf12″＋f2′＋xyf22″。

  • 第23题：

    问答题
    设z＝f（x2－y2，exy），其中f具有连续二阶偏导数，求∂z/∂x，∂z/∂y。

    正确答案：
    由复合函数的求导法则,得∂z/∂x=2xf1′+yexyf2′,∂z/∂y=-2yf1′+xexyf2′。
    解析： 暂无解析

  • 第24题：

    单选题
    设方程x＋z＝yf（x2－z2）（其中f可微）确定了z＝z（x，y），则z∂z/∂x＋y∂z/∂y＝（　　）。
    A

    x

    B

    y

    C

    z

    D

    yf（x2－y2）


    正确答案： D
    解析：
    由x＋z＝yf（x2－z2），可得∂z/∂x＝－（1－y·2xf′）/（1＋2yzf′），∂z/∂y＝－（－f）/（1＋2yzf′），故有（z∂z/∂x）＋（y∂z/∂y）＝（x－yf＋2xyzf′＋yf）/（1＋2yzf′）＝x。

相关内容