单选题已知函数y＝3x2的一条积分曲线过（1，1）点，则其积分曲线的方程为（　　）。A y＝x3B y＝x3＋1C y＝x3＋2D y＝x3＋C

题目
单选题
已知函数y＝3x2的一条积分曲线过（1，1）点，则其积分曲线的方程为（　　）。
A

y＝x3

B

y＝x3＋1

C

y＝x3＋2

D

y＝x3＋C

相似考题

1.曲线y=x+ln x在点（1，1）处的切线方程为________________.

2.已知消费函数C=30+0.8Y, 投资函数I=60-10r,求IS曲线方程.

3.过原点作曲线y=ex的切线，则切线的方程为(62)。A．y=exB．y=exC．y=xD．

4.已知函数f（x）=x3 +ax2+b，曲线y=f（x）在点（1，1）处的切线为y=x．（I）求a，b；（II）求f（x）的单调区间，并说明它在各区间的单调性．

更多“已知函数y＝3x2的一条积分曲线过（1，1）点，则其积分曲线的方程为（　　）。”相关问题

  • 第1题：

    已知曲线y=x3-3x2-1，过点(1，-3)作其切线，求切线方程。


    正确答案：

    y′=3x2-6x，当x=1时，y=1-3-1=-3，即点（1，-3）在曲线上。可知此切线的斜率为k=3×12-6×1=-3，由点斜式可知，此切线的方程为y-(-3)=-3(x-1)即为y=-3x。

  • 第2题：

    设L是抛物线y=x2上从点A（1，1）到点O（0，0）的有向弧线，则对坐标的曲线积分



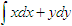
    等于（　　）。

    A、 0
    B、 1
    C、 -1
    D、 2

    答案：C
    解析：
    选择x的积分路线，有：

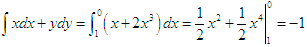
  • 第3题：

    曲线通过(1,1)点，且此曲线在[1,x]上所形成的曲边梯形面积的值等于该曲线终点的横坐标x与纵坐标y之比的两倍减去2，其中x>1，y>0。则当y x=1=1时的曲线方程为：


    答案：A
    解析：
    提示:把方程变形，得到可分离变量的方程，求通解、特解。解法如下：
    y3=2(y-xy') ,y3=2y-2xy', 2xy'=2y-y3

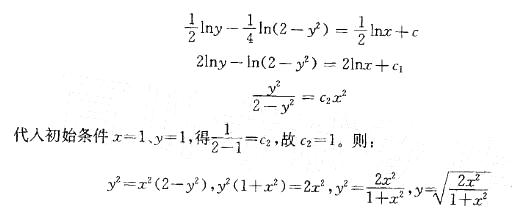
  • 第4题：

    曲线x2+y2=2x在点(1，1)处的切线方程为.


    答案：
    解析：
    【答案】y=1【考情点拨】本题考查了曲线上一点处的切线方程的知识点．
    【应试指导】由x2+y2=2x，两边对x求导得2x+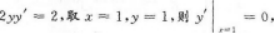

  • 第5题：

    已知曲线L的方程为y=1-｜x｜(x∈［-1，1］)，起点是(-1，0)，终点为(1，0)，则曲线积分________.


    答案：1、0.
    解析：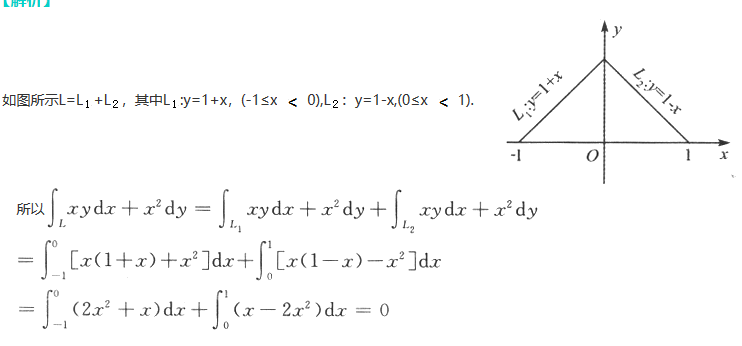

  • 第6题：

    设曲线y=y（x）过（0，0）点，M是曲线上任意一点，MP是法线段，P点在x轴上，已知MP的中点在抛物线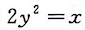，求此曲线的方程。


    答案：
    解析：

  • 第7题：

    求函数y=x-lnx的单调区间，并求该曲线在点(1，1)处的切线l的方程．


    答案：
    解析：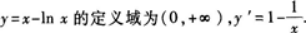


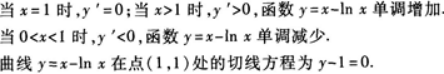
    【评析】求函数f(x)的单调区间，应先判定函数的定义域．求出函数的驻点，即y′=0的点；求出y的不可导的点，再找出y′>0时x的取值范围，这个范围可能是一个区间，也可能为几个区间．

  • 第8题：

    设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．

    • A、2
    • B、1/2
    • C、1/3
    • D、1/4

    正确答案:C

  • 第9题：

    单选题
    设L是曲线y=lnx上从点（1，0）到点（e，1）的一段弧，则曲线积分=（）。
    A

    e

    B

    e-1

    C

    e+1

    D

    0


    正确答案： A
    解析： 暂无解析

  • 第10题：

    单选题
    设C为抛物线y2=x上从点0（0，0）到点P（1，1）的一段弧，则曲线积分的值是（）．
    A

    2

    B

    1/2

    C

    1/3

    D

    1/4


    正确答案： C
    解析： 暂无解析

  • 第11题：

    填空题
    设函数y＝f（x）由方程e2x＋y－cos（xy）＝e－1所确定，则曲线y＝f（x）在点（0，1）处的法线方程为____。

    正确答案： y-1=x/2
    解析：
    e2x＋y－cos（xy）＝e－1方程两边对x求导，得e2x＋y（2＋y′）＋sin（xy）·（y＋xy′）＝0。当x＝0时，y＝1，y′＝－2，因此，法线方程为y－1＝x/2。

  • 第12题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    x－y＝0

    B

    x＋y＝0

    C

    －x－y＝0

    D

    －x＋y＝0


    正确答案： C
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第13题：

    如果曲线y=f(x)在点（x,y）处的切线斜率与x2成正比，并且此曲线过点（1，-3）和（2，11），则此曲线方程为（ ）。

    A. y=x3-2

    B. y=2x3-5

    C. y=x2-2

    D. y=2x2-5


    正确答案：B

    由曲线过点（1，-3）排除A、C项。由此曲线过点（2，11）排除D，故选B。y=2x3-5显然过点（1,-3）和（2，11），且它在（x,y）处的切线斜率为6x2，显然满足与x2成正比。

  • 第14题：

    设方程y´´-4y´+3y=0的某一积分曲线，它在点(0，2)处与直线x-y+2=0相切，则该积分曲线的方程是( ).

    A.
    B.
    C.
    D.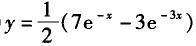

    答案：B
    解析：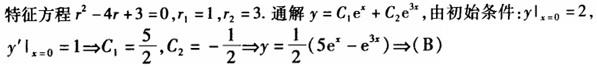

  • 第15题：

    设L为连接(0,0)点与(1,1)点的抛物线y =x2 ，则对弧长的曲线积分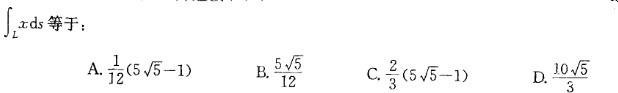


    答案：A
    解析：
    提示:利用对弧长的曲线积分方法计算。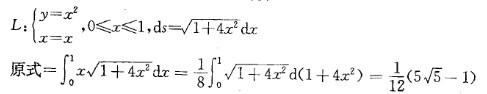

  • 第16题：

    计算曲线积分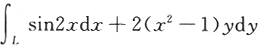，其中L是曲线y=sinx上从点(0，0)到点(π，0)的一段.


    答案：
    解析：
    【分析】利用曲线的参数方程直接转化为定积分计算或添加线段使之形成封闭曲线，再用格林公式，而添加线段上用参数法.

  • 第17题：

    设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.


    答案：1、2(ln2-1)
    解析：

  • 第18题：

    已知曲线y=x2+x-2的切线ι斜率为3，则ι的方程为_________．


    答案：
    解析：
    【答案】3x-y-3=0【考情点拨】本题考查了切线的知识点．

  • 第19题：

    已知对称轴为坐标轴的双曲线有一条渐近线的方程为2x-y=0，则双曲线的离心率为


    答案：
    解析：

  • 第20题：

    问答题
    已知曲线y=x3-3x2-1，过点(1，-3)作其切线，求切线方程。

    正确答案： 解：y′=3x2-6x，当x=1时，y=1-3-1=-3，即点（1，-3）在曲线上。可知此切线的斜率为k=3×12-6×1=-3，由点斜式可知，此切线的方程为y-(-3)=-3(x-1)即为y=-3x。
    解析： 暂无解析

  • 第21题：

    填空题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为____。

    正确答案： x-y=0
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

  • 第22题：

    单选题
    若曲线C上点的坐标都是方程f（x，y）＝0的解，则下列判断中正确的是（　　）．
    A

    曲线C的方程是f（x，y）＝0

    B

    以方程f（x，y）＝0的解为坐标的点都在曲线C上

    C

    方程f（x，y）＝0的曲线是C

    D

    方程f（x，y）＝0表示的曲线不一定是C


    正确答案： C
    解析：
    AC两项，说曲线C是方程f（x，y）＝0的曲线，方程f（x，y）＝0是曲线C的方程必须同时具备定义中的两个条件：①曲线上的点的坐标都是这个方程的解；②以这个方程的解为坐标的点都在这条曲线上．此题仅给出定义中的条件之一；B项，与题干所给条件无关．

  • 第23题：

    单选题
    函数y＝f（x）是由方程xy＋2lnx＝y4所确定，则曲线y＝f（x）在点（1，1）处的切线方程为（　　）。
    A

    －x－y＝0

    B

    x－y－1＝0

    C

    x－y＝0

    D

    x＋y＝0


    正确答案： A
    解析：
    xy＋2lnx＝y4两端对x求导，得y＋xy′＋2/x＝4y3·y′。x＝1时，y＝1，y′（1）＝1，则切线方程为y－1＝x－1，即x－y＝0。

相关内容