单选题具有特解y1＝e－x，y2＝2xe－x，y3＝3ex的三阶常系数齐次线性方程是（　　）。A y‴－y″－y′＋y＝0B y‴＋y″－y′－y＝0C y‴－6y″＋11y′－6y＝0D y‴－2y″－y′＋2y＝0

题目
单选题
具有特解y1＝e－x，y2＝2xe－x，y3＝3ex的三阶常系数齐次线性方程是（　　）。
A

y‴－y″－y′＋y＝0

B

y‴＋y″－y′－y＝0

C

y‴－6y″＋11y′－6y＝0

D

y‴－2y″－y′＋2y＝0

相似考题

1.下面的程序使用了函数指针，其运行结果是______。 #include＜stdio.h＞#include＜math.h＞int f1（int a）{return a*a;}int f2（int a）{return a*a*a;}void main（ ）{int x=3,y1,y2,y3,y4;f=f1;y1=（*f）（x）;y2=f1（x）;f=f2;y3=f（x）;y4=f2（x）;printf（"y1=%d,y2=%d,y3=%d,y4=%d\n",y1,y2,y3,y4）;}A.y1=27,y2=9,y3=9,y4=27 B.y1=9,y2=9,y3=27,y4=27 C.y1=9,y2=27,y3=9,y4=27 D.y1=27,y2=27,y3=9,y4=9

2.A、 y1=x，y2=ex B、 y1=e-x，y2=ex C、 y1=e-x，y2=xe-x D、 y1=ex，y2=xex

3.以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是: A. y''-2y'-3y=0 B. y''+2y'-3y=0 C. y''-3y'+2y=0 D. y''+2y'+y=0

4.仔细阅读下面程序，请给出运行结果（ ）。#include#includeint f1（int x）{return x*x；}int f2（int x）{return x*x*x；}main（ ）{int x=3,y1,y2,y3,y4；int（*f）（ ）；f=f1；y1=（*f）（x）；y2=f1（x）；f=f2；y3=f（x）；y4=f2（x）；printf（“y1=%d，y2=%d，y3=%d，y4=%d\n”，y1，y2，y3，y4）；}A.y1=9,y2=9,y3=27,y4=27 B.y1=3,y2=9,y3=27,y4=9 C.y1=3,y2=3,y3=9,y4=9 D.y1=3,y2=9,y3=9,y4=27

更多“单选题具有特解y1＝e－x，y2＝2xe－x，y3＝3ex的三阶常系数齐次线性方程是（　　）。A y‴－y″－y′＋y＝0B y‴＋y″－y′－y＝0C y‴－6y″＋11y′－6y＝0D y‴－2y″－y′＋2y＝0”相关问题

  • 第1题：

    微分方程y''-6y'+9y=0在初始条件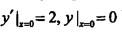下的特解为（ ）


    答案：D
    解析：
    提示：这是二阶常系数线性齐次方程。

  • 第2题：

    下列微分方程是线性微分方程的是（）。

    • A、x（y’）2+y=ex
    • B、xy"+xy’+y=cosx
    • C、y3y"+y’+2y=0
    • D、y"+2y"+y2=0

    正确答案:B

  • 第3题：

    以为特解的二阶线性常系数齐次微分方程是（）。

    • A、y＂-2y＇-3y=0
    • B、y＂+2y＇-3y=0
    • C、y＂-3y＇+2y=0
    • D、y＂-2y＇-3y=0

    正确答案:B

  • 第4题：

    单选题
    以y1＝ex，y2＝e2xcosx为特解的最低阶数的常系数线性齐次方程为（　　）。
    A

    y‴－5y″－9y′－5y＝0

    B

    y‴－5y″－5y′－5y＝0

    C

    y‴－5y″＋9y′－5y＝0

    D

    y‴－5y″＋5y′－5y＝0


    正确答案： A
    解析：
    由题意可知，r1＝1，r2，3＝2±i是其特征方程的根，则最低的齐次方程的阶数为3，则其特征方程为（r－1）（r－2－i）（r－2＋i）＝0，即（r－1）（r2－4r＋5）＝0，r3－5r2＋9r－5＝0。故满足题意的齐次方程为y‴－5y″＋9y′－5y＝0。

  • 第5题：

    单选题
    以y1＝ex，y2＝e－3x为特解的二阶线性常系数齐次微分方程是（　　）。[2012年真题]
    A

    y″－2y′－3y＝0

    B

    y″＋2y′－3y＝0

    C

    y″－3y′＋2y＝0

    D

    y″－2y′－3y＝0


    正确答案： B
    解析：
    因y1＝ex，y2＝e－3x是特解，故r1＝1，r2＝－3是特征方程的根，因而特征方程r2＋2r－3＝0。故二阶线性常系数齐次微分方程是：y″＋2y′－3y＝0。

  • 第6题：

    问答题
    设二阶线性微分方程y″＋P（x）y′＋Q（x）y＝f（x）的三个特解是y1＝x，y2＝ex，y3＝e2x，试求此方程满足条件y（0）＝1，y′（0）＝3的特解。

    正确答案：
    由题意可知,Y1=ex-x、Y2=e2x-x是原方程对应齐次方程的两个线性无关的解[因(ex-x)/(e2x-x)≠常数],故原方程的通解为y=C1(ex-x)+C2(e2x-x)+x,由y(0)=1,y′(0)=3,得C1=-1,C2=2。故所求原方程的特解为y=-(ex-x)+2(e2x-x)+x=2e2x-ex。
    解析： 暂无解析

  • 第7题：

    单选题
    具有待定特解形式为y=A1x+A2+B1ex的微分方程是下列中哪个方程（）？
    A

    y″+y′-2y=2+ex

    B

    y″-y′-2y=4x+2ex

    C

    y″-2y′+y=x+ex

    D

    y″-2y′=4+2ex


    正确答案： C
    解析： 暂无解析

  • 第8题：

    单选题
    设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（　　）。
    A

    y″＋2y′＋2y＝0

    B

    y″－2y′＋2y＝0

    C

    y″－2y′－2y＝0

    D

    y″＋2y′＋2y＝0


    正确答案： A
    解析：
    根据题中所给的通解y＝ex（c1sinx＋c2cosx）的结构可知，所求方程对应的特征根为λ1，2＝1±i，特征方程为[λ－（1＋i）][λ－（1－i）]＝λ2－2λ＋2＝0，则所求方程为y″－2y′＋2y＝0。

  • 第9题：

    具有待定特解形式为y=A1x+A2+B1ex的微分方程是下列中哪个方程（）？

    • A、y″+y′-2y=2+ex
    • B、y″-y′-2y=4x+2ex
    • C、y″-2y′+y=x+ex
    • D、y″-2y′=4+2ex

    正确答案:B

  • 第10题：

    在塔里木油田公司压井管汇现场待令工况正确的是（）。

    • A、Y2常关Y3常关Y4常开
    • B、Y2常关Y3常关Y4常关
    • C、Y2常开Y3常关Y4常开
    • D、Y2常关Y3常开Y4常关

    正确答案:B

  • 第11题：

    单选题
    以为特解的二阶线性常系数齐次微分方程是（）。
    A

    y＂-2y＇-3y=0

    B

    y＂+2y＇-3y=0

    C

    y＂-3y＇+2y=0

    D

    y＂-2y＇-3y=0


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    具有特解y1＝e－x，y2＝2xe－x，y3＝3ex的三阶常系数齐次线性方程是（　　）。
    A

    y‴－y″－y′＋y＝0

    B

    y‴＋y″－y′－y＝0

    C

    y‴－6y″＋11y′－6y＝0

    D

    y‴－2y″－y′＋2y＝0


    正确答案： C
    解析：
    由题设可知，该齐次方程的通解为y＝（C1＋C2x）e－x＋C3ex，则r＝－1是特征方程的二重特征根，r＝1是特征方程的单根，故其特征方程为（r＋1）2（r－1）＝0即r3＋r2－r－1＝0。故所求三阶常系数线性齐次方程为y‴＋y″－y′－y＝0。

  • 第13题：

    单选题
    （2012）以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：（）
    A

    y″-2y′-3y=0

    B

    y″+2y′-3y=0

    C

    y″-3y′+2y=0

    D

    y″+2y′+y=0


    正确答案： D
    解析： 暂无解析

  • 第14题：

    单选题
    函数y＝C1ex＋C2e－2x＋xex满足的一个微分方程是（　　）。
    A

    y″－y′－2y＝3xex

    B

    y″－y′－2y＝3ex

    C

    y″＋y′－2y＝3xex

    D

    y″＋y′－2y＝3ex


    正确答案： D
    解析：
    由函数y＝C1ex＋C2e－2x＋xex结合解的结构可知，y1＝ex及y2＝e－2x是所求非齐次方程对应齐次方程的解，y3＝xex是所求非齐次方程的一个特解。故对应特征方程的根为r1＝1，r2＝－2，特征方程为（r－1）（r＋2）＝r2＋r－2＝0。则齐次方程为y″＋y′－2y＝0。假设所求方程为y″＋y′－2y＝f（x），将y3＝xex代入得f（x）＝3ex。则所求方程为y″＋y′－2y＝3ex。

  • 第15题：

    单选题
    设y＝ex（c1sinx＋c2cosx）（c1、c2为任意常数）为某二阶常系数线性齐次微分方程的通解，则该方程为（　　）。
    A

    y″－y′＋y＝0

    B

    y″－2y′＋2y＝0

    C

    y″－2y′＝0

    D

    y′＋2y＝0


    正确答案： A
    解析：
    根据题中所给的通解y＝ex（c1sinx＋c2cosx）的结构可知，所求方程对应的特征根为λ1，2＝1±i，特征方程为[λ－（1＋i）][λ－（1－i）]＝λ2－2λ＋2＝0，则所求方程为y″－2y′＋2y＝0。

  • 第16题：

    单选题
    微分方程y″－2y′＋y＝0的两个线性无关的特解是（　　）。[2016年真题]
    A

    y1＝x，y2＝ex

    B

    y1＝e－x，y2＝ex

    C

    y1＝e－x，y2＝xe－x

    D

    y1＝ex，y2＝xex


    正确答案： D
    解析：
    本题中，二阶常系数线性微分方程的特征方程为：r2－2r＋1＝0，解得：r1＝r2＝1，故方程的通解为：y2＝ex（c1＋c2x），则两个线性无关解为c1ex、c2xex（c1、c2为常数）。

相关内容