单选题已知A为3×4矩阵，X=（x1，x2，x3，x4）T，AX=0有通解k（1，l，O，-1）T，其中k为任意常数，将A中去掉第i列（i=1，2，3，4）的矩阵记为Ai，则下列方程组中有非零解的是（ ）.A A1Y=0B A2Y=0C A3Y=0D A4Y=0
题目
A1Y=0
A2Y=0
A3Y=0
A4Y=0
相似考题
更多“单选题已知A为3×4矩阵，X=（x1，x2，x3，x4）T，AX=0有通解k（1，l，O，-1）T，其中k为任意常数，将A中去掉第i列（i=1，2，3，4）的矩阵记为Ai，则下列方程组中有非零解的是（ ）.A A1Y=0B A2Y=0C A3Y=0D A4Y=0”相关问题
-
第1题：
下列程序的输出结果是includevoid main( ){char*str="12123434";int xl=0,x2=0,x3= 下列程序的输出结果是 #include＜iostream.h＞ void main( ) {char*str="12123434"； int xl=0，x2=0，x3=0，x4=0，i; for(i=0；str[i]!='\0';i++) switch(str[i]) {case'1'：x4++； case'2'：x3++； case'3'：x2++； case'4'：x1++； } cout＜＜x1＜＜"，"＜＜x2＜＜"，"＜＜x3＜＜"，"＜＜x4； }
A．8，6，4，1
B．8，6，3，2
C．8，8，4，1
D．8，6，4，2
正确答案：D
解析：本题考查循环的嵌套。只要注意在C++语言中，系统在字符指针的最后位置会增加一个字符串结束符'\0',执行8次for循环，再根据switch语句中的条件易知答案。注意：c++中各种条件判断，循环语句的用法。 -
第2题：
已知有一维数组A(0..m*n-1]，若要对应为m行、n列的矩阵，则下面的对应关系(4)可将元素A[k](0≤k＜m*n)表示成矩阵的第i行、第j列的元素(0≤i＜m，0≤j＜n)。
A．i=k/n,j=k%m
B．i=k/m,j=K%m
C．i=k/n,j=k%n
D．i=k/m,j=k%n
正确答案：C
解析：此题是求一维数组向二维数组转化的问题。最原始的方法就是把数组A的前n个元素放到数组B的第一行，数组A的第n个元素放到数组B的第二行中，依次类推，数组A的最后n个元素放到数组B的最后一行中。求且[幻在数组B中的位置，应先确定A[k]处在哪一行，显然应该是k/n行，然后再确定处在k/n行的哪一列，显然是k%n列。 -
第3题：
下列程序的输出结果是 #include void main( ) { char * str="12123434"； int x1=0，x2=0，x3=0，x4=0，i； for(i=0；str[i]!='\0';i++) switch(str[i]) { case'1'：x4++； case'2'：x3++； case'3'：x2++； case'4'：x1++； } cout ＜ ＜ x1 ＜ ＜ "，" ＜ ＜ x2
A．8，6，4，1
B．8，6，3，2
C．8，8，4，1
D．8，6，4，2
正确答案：D
解析：本题考查循环的嵌套。只要注意在c++语言中，系统在字符指针的最后位置会增加一个字符串结束符'\0'，执行8次for循环，再根据switch语句中的条件易知答案。注意：C++中各种条件判断，循环语句的用法。 -
第4题：
已知3阶矩阵A的第一行是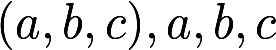
不全为零，矩阵 
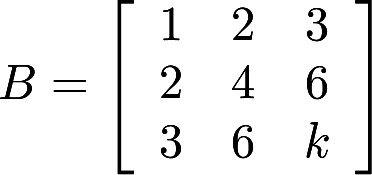（k为常数），且AB=0, 求线性方程组Ax=0的通解答案：解析：
-
第5题：
设β1，β2是线性方程组Ax=b的两个不同的解，a1、a2是导出组Ax=0的基础解系，k1、k2是任意常数，则Ax=b的通解是：
答案：C解析：提示 非齐次方程组的通解y=y(齐次方程的通解)+y *(非齐次方程的一个特解)，可验证(1/2)(β1+β2)是Ax=b的一个特解。
因为β1,β2是线性方程组Ax=6的两个不同的解
A[(1/2)(β1+β2)]=(1/2)Aβ1+(1/2)Aβ2
又已知a1，a2为导出组Ax=0的基础解系，可知a1，a2是Ax=0解，同样可验证a1-a2也是Ax=0的解，A(a1-a2)=Aa1-Aa2=0。
还可验证a1,a1-a2线性无关
故齐次方程组的通解y=k1a1+k2(a1-a2)
y*=(1/2)(β1+β2)=是Ax=b的一特解
所以Ax=b的通解为y=(1/2)(β1+β2)+k1a1+k2(a1-a2) -
第6题：
设β1，β2是线性方程组Ax=b的两个不同的解，α1、α2是导出组Ax=0的基础解系，k1,k2是任意常数，则Ax=b的通解是：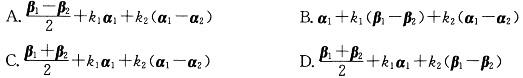
答案：C解析：
-
第7题：
已知有一维数组A[0.m×n-1]，若要对应为m行n列的矩阵，则下面的对应关系()，可将元素A[k](O≤＜k≤＜m×n)表示成矩阵的第i行、第j列的元素(0≤i≤m，0匀≤n)。A. i=k/n，j=k%m
B.i=k/m，j=k%m
C.i=k/n，j=k%n
D.i=k/m，j=k%n答案：C解析：矩阵每一行有n个元素，则第i+l行、第j+l到的元素～在A中是第n×i+j+l个元素，对应的下标k=nXi+j(因为下标从0开始)。反过来：i=k/n，j=k%n。 -
第8题：
已知4元非齐次线性方程组Ax=b的系数矩阵的秩等于3，且η1，η2，η3是3个不同的解向量，则通解是( ).A.x=k1(η-η2)+η3
B.x=k1η1+k2η2+η3
C.x=k1η1+k2η2+k3η3
D.x=k1(η+η2)+η3答案：A解析：由n=4，r=3得s=1。ηη2是 Ax=0的基础解系 -
第9题：
没A是n*n常数矩阵（n>1），X是由未知数X1，X2，…，Xn组成的列向量，B是由常数b1，b2，…，bn组成的列向量，线性方程组AX=B有唯一解的充分必要条件不是（）。
- A、A的秩等于n
- B、A的秩不等于0
- C、A的行列式值不等于0
- D、A存在逆矩阵
正确答案:B -
第10题：
电液转辙机无定位表示，定位向反位操纵不动，电液转辙机分线盘X1至组合侧面05-1之间断线，以下现象符合该故障的是（）。
- A、X2与X1、X3、X4间电压为AC0V
- B、X1与X3、X4间电压为AC0V
- C、X2与X1、X3、X4间电压为AC105V
- D、X1与X3、X4间电压为AC105V
正确答案:A,B -
第11题：
单选题设α1，α2，α3，α4是4维非零列向量组，A=（α1，α2，α3，α4），A*是A的伴随矩阵，已知方程组AX=0的基础解系为k（1，0，2，0）T，则方程组A*X=0的基础解系为（ ）.Aα1，α2，α3
Bα1+α2，α2+α3，3α3
Cα2，α3，α4
Dα1+α2，α2+α3，α3+α4，α4+α1
正确答案： D解析：
由AX=0的基础解系仅含有一个解向量，知r（A）=4-1=3，所以r（A*）=1，则AX=0A*X=0的基础解系含三个解向量．
又（α1，α2，α3，α4）（1，0，2，0）T=0，即α1+2α3=0，知（α1，α3）线性相关，所以方程组A*X=0的基础解系为α2，α3，α4． -
第12题：
单选题n阶矩阵A的伴随矩阵为A*，齐次线性方程组AX=O有两个线性无关的解，则（ ）.AA*X=0的解均是AX=0的解
BAX=0的解均是A*X=O的解
CAX=0与A*X=0无非零公共解
DAX=0与A*X=O仅有2个非零公共解
正确答案： B解析：
由齐次方程组AX=0有两个线性无关的解向量，知方程组AX=0的基础解系所含解向量的个数为n-r（A）≥2，即r（A）≤n-2<n-1．由矩阵A与其伴随矩阵秩的关系，知r（A*）=0，即A*=0．所以任意n维列向量均是方程组A*X=0的解，故方程组AX=0的解均是A*X=0的解． -
第13题：
下列程序的输出结果是includevoid main(){char*str="12123434"; int x1=0,x2=0,x3= 下列程序的输出结果是 #include＜iostream．h＞ void main() { char*str="12123434"； int x1=0，x2=0，x3=0，x4=0，i; for(i=0；str[i]!=‘\0’；i++) switch(str[i]) { case'l'：x4++； case'2'：X3++； case'3'：x2++； case'4'：X1++； } cout ＜＜ X1 ＜＜ " ，" ＜＜ x2 ＜＜ " ’" ＜＜ x3 ＜＜ " ，" ＜＜ X4； }
A．8，6，4，1
B．8，6，3，2
C．8，8，4，1
D．8，6，4，2
正确答案：D
解析：本题考查循环的嵌套。只要注意在C++语言中，系统在字符指针的最后位置会增加一个字符串结束符‘、0’，执行8次for循环，再根据switch语句中的条件易知答案。注意：C++中各种条件判断，循环语句的用法。 -
第14题：
下列程序的输出结果是includevoid main(){char*str="12123434";int x1=0,x2=0,x3=0 下列程序的输出结果是 #include＜iostream.h＞ void main() ｛char*str＝"12123434"; int x1＝0,x2＝0,x3＝0,x4＝0,i; for(i＝0;str[i]!＝'\0';i++) switch(str[i]) ｛case'1'：x4++; case'2'：X3++; case'3'：X2++; case'4'：X1++; ｝ cout＜＜X1＜＜","＜
A．8,6,4,1
B．8,6,3,2
C．8,8,4,1
D．8,6,4,2
正确答案：D
-
第15题：
设随机变量X1,X2,X3,X4独立同分布,且Xi～
（i=1,2,3,4）,求X=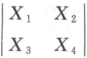
的概率分布.答案：解析：
-
第16题：
方程组
的解为( )。A、x1=-18，x2=0，x3=0
B、x1=0，x2=0，x3=3
C、x1=2，x2=1，x3=3
D、x1=0，x2=6，x3=0答案：C解析：经验证，(C)是方程组的解，或对增广矩阵进行初等行变换，增广矩阵
可见方程组的解为x3=3，x2=1，x1=2 -
第17题：
设B是三阶非零矩阵，已知B的每一列都是方程组
的解，则t等于
A.0
B.2
C.1
D.-1答案：D解析：提示：已知条件B是三阶非零矩阵，而B的每一列都是方程组的解，可知齐次方程Ax=0有非零解。所以齐次方程组的系数行列式为0，
式，t=1。 -
第18题：
设A是4×5矩阵，ξ1，ξ2是齐次线性方程组Ax=0的基础解系，则下列结论正确的是( ).A.ξ1-ξ2，ξ1+2ξ2也是Ax=0的基础解系
B.k1ξ1+k1ξ2是Ax=0的通解
C.k1ξ1+ξ2是Ax=0的通解
D.ξ1-ξ2，ξ2-ξ1也是Ax=0的基础解系答案：A解析：由题设知道，n=5，s=n-r=2，r=3.B不正确，因为k1ξ1+k1ξ2=k1(ξ2+ξ1)只含有一个不定常数，同样理由说明C也不正确.D不正确，因为(ξ1-ξ2)+(ξ1+ξ2)=0，这表明ξ1-ξ2与ξ2-ξ1线性相关.A正确，因为ξ1-ξ2与ξ1+2ξ2都是Ax=0的解，且它 们线性无关，故选A. -
第19题：
已知al,a2，a3，a4是四维非零列向量，记A=(a1，a2,a3，a4)，A+是A的伴随矩阵，若齐次方程组AX=0的基础解系为(1，0,-2，0)T，则AX=0的基础解系为( )。A、al a2
B、a1 a3
C、al a2 a3
D、a2 a3 a4答案：D解析：AX=0的基础解系只含有一个向量，所以矩阵A的秩为3，所以A存在不为0的3阶子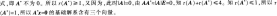
即a1-2a3=0，所以a1与a3线性相关。而方程组的基本解系必须是线性相关的向量，所以正确答案为D。 -
第20题：
设B是3阶非零矩阵，已知B的每一列都是方程组
的解，则t等于（ ）。
A. 0 B. 2 C. -1 D. 1答案：D解析：提示：由条件知齐次方程组有非零解，故系数行列式等于零，
，得t = 1,故选D。 -
第21题：
某事故树的最小径集为：P1={X1，X3}，P2={X1，X5}，P3={X2，X3，X4}，P4={X2，X4，X6}，则基本事件X1、X2、X3的结构重要程度大小排序正确的是（）
- A、 I（1）＞I（3）＞I（2）
- B、 I（1）=I（2）= I（3）
- C、 I（1）＜I（2）＜I（3）
- D、 I（2）＞I（1）＞I（3）
正确答案:A -
第22题：
单选题设n阶矩阵A的各行元素之和均为零，且A的秩为n－1，则线性方程组AX(→)＝0(→)的通解为（ ）。AX＝k（1，1，…，1）T
BX＝k（1，1，…，－1）T
CX＝k（－1，1，…，1）T
DX＝k（－1，1，…，－1）T
正确答案： C解析：
由r（A）＝n－1，知方程组AX＝0的基础解系只含有n－（n－1）＝1个解向量。又矩阵A的各行元素之和为0，知（1，1，…，1）T，为AX＝0的非零解，则方程组AX＝0的通解为X＝k（1，1，…，1）T。 -
第23题：
单选题已知A为3×4矩阵，X=（x1，x2，x3，x4）T，AX=0有通解k（1，l，O，-1）T，其中k为任意常数，将A中去掉第i列（i=1，2，3，4）的矩阵记为Ai，则下列方程组中有非零解的是（ ）.AA1Y=0
BA2Y=0
CA3Y=0
DA4Y=0
正确答案： D解析：
由A3×4X=0有通解k（1，l，O，-1）T，对A以列分块有A=（α1，α2，α3，α4），则α1+α2-α4=0，即A3Y=0有非零解（1，l，-1）T． -
第24题：
单选题已知A为3×4矩阵，X(→)＝（x1，x2，x3，x4）T，AX(→)＝0(→)有通解k（1，l，0，－1）T，其中k为任意常数，将A中去掉第i列（i＝1，2，3，4）的矩阵记为Ai，则下列方程组中有非零解的是（ ）。AA1Y＝0
BA2Y＝0
CA3Y＝0
DA4Y＝0
正确答案： C解析：
由A3×4X＝0有通解k（1，l，0，－1）T，对A以列分块有A＝（α1，α2，α3，α4），则α1＋α2－α4＝0，即A3Y＝0有非零解（1，l，－1）T。