单选题曲线y=（x-l）2（x-3）2的拐点的个数为（　　）A 0B 1C 2D 3

题目
单选题
曲线y=（x-l）2（x-3）2的拐点的个数为（　　）
A

0

B

1

C

2

D

3

相似考题

1.有以下程序#include <stdio.h>main( ){ int a[ ]={1,2,3,4},y,*p=&a[3];--p; y=*p; printf("y=%d\n",y);}程序的运行结果是A)y=0B)y=1C)y=2D)y=3

2.f(x)=1／x＋[e^(1／2－x)]／(x－1)的间断点的个数是()A、0B、1C、2D、3

3.线性规划要求决策变量个数为()。A、>=0B、>=1C、>=2D、无要求

4.曲线y =x3－3x2－x的拐点坐标为____。

更多“单选题曲线y=（x-l）2（x-3）2的拐点的个数为（　　）A 0B 1C 2D 3”相关问题

  • 第1题：

    函数f(x)=x2－9／x－3的间断点为()。

    A、x=0

    B、x=1

    C、x=2

    D、x=3


    答案：A

    解析：间断点即x取不到的点，即x在此处无意义。由题意可知，原函数中含有分数，x作为分母，不能取0，所以选择A项。

  • 第2题：

    树支组成的网络回路个数是()。

    A、0

    B、1

    C、2

    D、3


    参考答案：A

  • 第3题：

    曲线y=(x-1)(x-2)^2(x-3)^3(x-4)^4的拐点是



    A.A(1，0)
    B.(2，0)
    C.(3,0)
    D.(4,0)

    答案：C
    解析：
    (方法一)图示法：由曲线方程y=(x-1)(x-2)^2(x-3)^3(x-4)^4可知，该曲线和x轴有四个交点，即x=1，x=2，x=3，x=4，且在x=2取极大值，x=4取极小值，则拐点只能在另外两个点上，由下图不难看出(3，0)为拐点，故应选(C).

    　(方法二)记g(x)=(x-1)(x-2)^2(x-4)^4，则y-(x-3)^3g(x)
    　　设g(x)在x=3处的泰勒展开式为g(x)=a0+a1(x-3)+…
    　　则y=a0(x-3)^3+a0(x-3)^4+…
    　　由该式可知y"(3)=0，y'"(3)=a0·3！≠0
    　　因为a0=g(3)≠0.由拐点的第二充分条件知，(3，0)为拐点

  • 第4题：

    设函数f(x)在(一∞，+∞)内连续，其中二阶导数f”(x)的图形如图所示，则曲线y(x)的拐点的个数为( )个。

    A、0
    B、1
    C、2
    D、3

    答案：C
    解析：
    拐点出现在二阶导数等于零，或二阶导数不存在的数，并且在这点的左右两侧二阶导函数异号。因此，由f”(x)的图形可得，曲线y=(x)存在两个拐点。

  • 第5题：

    设函数f(χ)在(-∞，+∞)内连续，其中二阶导数f”(χ)的图形如图所示，则曲线y=f(χ)的拐点的个数为( )。

    A、0
    B、1
    C、2
    D、3

    答案：C
    解析：
    拐点出现在二阶导数等于零，或二阶导数不存在的数，并且在这点的左右两侧二阶导函数异号。因此，由f〞(x)的图形可得，曲线y=f（x）存在两个拐点。

  • 第6题：

    曲线y=x3-6x2+3x+4的拐点为_________．


    答案：
    解析：
    【答案】(2，-6)【考情点拨】本题考查了拐点的知识点．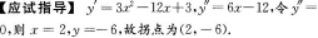

  • 第7题：

    已知x=123，那么执行语句y=x/10Mod10后，变量y的值是（）。

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:C

  • 第8题：

    假设Y是一个数值型变量，那么下列表达式中可以用来测试Y是否为偶数的是（）。

    • A、INT（Y/2）=Y/2
    • B、YMod2=1
    • C、Abs（Y/2）=Y/2
    • D、INT（Y/3）=Y/3

    正确答案:A

  • 第9题：

    max（[0，1，2，3]）的值为（）

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:D

  • 第10题：

    点（0，1）是曲线y=ax3+bx+c的拐点，则a、b、c的值分别为（）

    • A、a=1，b=-3，c=-2
    • B、a≠0的实数，b为任意实数，c=1
    • C、a=1，b=0，c=2
    • D、a=0、b为任意实数，c=1

    正确答案:B

  • 第11题：

    函数少=（5_X）X3的极值可疑点的个数是（）。

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:C

  • 第12题：

    单选题
    设y＝（4x＋4）/x2－2，则曲线在拐点处的切线方程为（　　）。
    A

    y＋26/9＝－4（x＋3）/27

    B

    y＋26/9＝4（x＋3）/27

    C

    y＋26/9＝－4（x－3）/27

    D

    y＋26/9＝4（x－3）/27


    正确答案： D
    解析：
    先求方程的拐点，原方程为y＝（4x＋4）/x2－2，则有y′＝－4/x2－8/x3，y″＝8/x3＋24/x4＝8（x＋3）/x4＝0，得x＝－3。x＜－3时，y″＜0；x＞－3时，y″＞0。而y′（－3）＝－4/27，y（－3）＝－26/9，故拐点处的切线方程为y＋26/9＝－4（x＋3）/27。

  • 第13题：

    设f(x)=x(x＋1)(x＋2)(x＋3),则f'(x)=0的正根的个数为()

    A、0

    B、1

    C、2

    D、3


    答案：A

    解析：f(x)=x(x＋1)(x＋2)(x＋3)=x^4+6x^3+11x^2+6x，所以f'(x)=4x^3+18x^2+22x+6，因为求f'(x)=0的正根，即x>0，所以当x>0时，f'(x)=4x^3+18x^2+22x+6>0，所以f'(x)=0没有正根。故选A。


  • 第14题：

    曲线y=x3-3x2+5x-4的拐点坐标为______．


    答案：
    解析：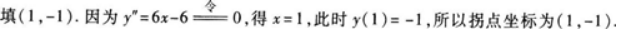

  • 第15题：

    设空间区域V：x2+y2+z2≤R2，则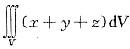

    =( )。


    A、0
    B、1
    C、2
    D、3

    答案：A
    解析：
    由于V关于三个坐标面都对称，而被积函数关于一个变量为奇函数，因此积分为零

  • 第16题：

    函数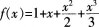的图象与x轴交点的个数是( )。

    A、0
    B、1
    C、2
    D、3

    答案：B
    解析：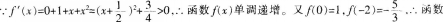
    f(x)的图象与x轴有且只有一个交点。故选B。

  • 第17题：

    设函数f(χ)在(-∞，+∞)内连续，其中二阶导数f”(χ)的图形如图所示，则曲线y=f(χ)的拐点的个数为( )。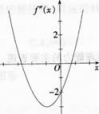

    A、0
    B、1
    C、2
    D、3

    答案：C
    解析：
    拐点出现在二阶导数等于零，或二阶导数不存在的数，并且在这点的左右两侧二阶导函数异号。因此，由f〞(x)的图形可得，曲线y=f（x）存在两个拐点。

  • 第18题：

    决定Poisson分布图型的参数个数为（）

    • A、0
    • B、1
    • C、2
    • D、3
    • E、4

    正确答案:B

  • 第19题：

    若main（）函数带参数，参数个数最多是（）

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:C

  • 第20题：

    异步串行传输中起始位的个数是（）位。

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:B

  • 第21题：

    y=3-3//2，则x的值是（）

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:C

  • 第22题：

    OTUk中的k可以是以下哪个数字（）

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:B,C,D

  • 第23题：

    若步冷曲线出现平台，此时体系的条件自由度数为（）

    • A、0
    • B、1
    • C、2
    • D、3

    正确答案:A

相关内容