单选题矩阵A在（　　）时秩改变。A 转置B 初等变换C 乘以奇异矩阵D 乘以非奇异矩阵

题目
单选题
矩阵A在（　　）时秩改变。
A

转置

B

初等变换

C

乘以奇异矩阵

D

乘以非奇异矩阵

相似考题

1.若A是____,则A必为方阵。A.对称矩阵B.可逆矩阵C.n阶矩阵的转置矩阵D.线性方程组的系数矩阵

2.设A为非奇异对称矩阵,则____仍为对称矩阵。A.A的转置B.A的逆矩阵C.3AD.A与A的转置的乘积

3.机器人力雅可比矩阵和速度雅可比矩阵之间的关系是()。A、转置B、相等C、互逆D、转置再互逆

4.若A是____,则其转置与它本身相等。A.对角矩阵B.三角形矩阵C.可逆矩阵D.对称矩阵

参考答案和解析
正确答案： C
解析：
A项，对矩阵转置不改变矩阵的秩，即r（A）＝r（AT）；
B项，初等变换不该变矩阵的秩；
D项，乘以非奇异矩阵相当于对A进行若干次初等变换，不改变矩阵的秩。
更多“单选题矩阵A在（　　）时秩改变。A 转置B 初等变换C 乘以奇异矩阵D 乘以非奇异矩阵”相关问题

  • 第1题：

    下列命题不正确的是()

    A、转置运算不改变方阵A的行列式值和秩

    B、若m

    C、已知同阶方阵A，B和C满足AB=AC，若A是非奇异阵，则B=C

    D、若矩阵A的列向量线性相关，则A的行向量也线性相关


    参考答案：D

  • 第2题：

    三阶矩阵A的特征值为－2,1,3,则下列矩阵中为非奇异矩阵的是().

    A.2E-A

    B.2E+A

    C.E-A

    D.A-3E


    参考答案：

  • 第3题：

    对于对称矩阵A与B,求出非奇异矩阵C,使CTAC=B.


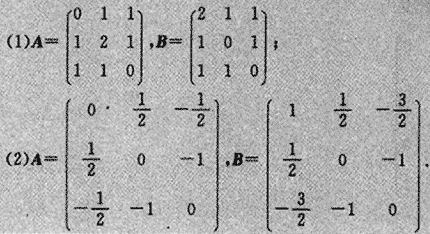    参考答案：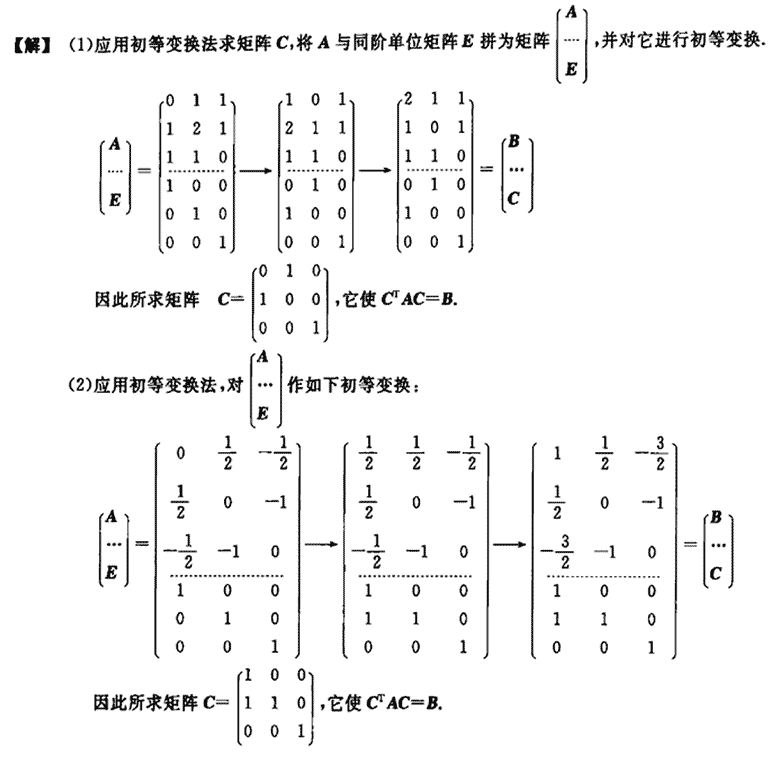

  • 第4题：

    设α，β为三维列向量，矩阵A=αα^T+ββ^T，其中α^T，β^T分别是α，β的转置.证明：
    　　(Ⅰ)秩r(A)≤2；
    　　(Ⅱ)若α，β线性相关，则秩r(A)<2.


    答案：
    解析：
    【证明】(Ⅰ)因为α，β为三维列向量，那么αα^T和ββ^T都是三阶矩阵，
    且秩r(αα^T)≤1，r(ββ^T)≤1.
    那么，r(A)=r(αα^T+ββ^T)≤r(αα^T)+r(ββ^T)≤2.
    (Ⅱ)由于α，β线性相关，不妨设α=kβ，于是
    r(A)=r(αα^T+ββ^T)=r((1+k^2)ββ^T)≤r(β)≤1<2.
    【评注】本题考查矩阵秩的性质公式.
    (Ⅰ)中有两个基本知识点：①r(αα^T)≤1和②r(A+B)≤r(A)+r(B).
    (Ⅱ)中有两个基本知识点：①α，β线性相关的几何意义和②r(kA)=r(A)，k≠0.
    注意，如果分块矩阵比较熟悉，本题的(Ⅰ)也可如下处理：
    因为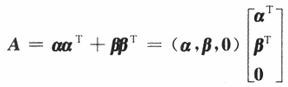

    那么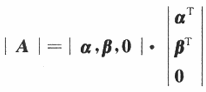
    从而r(A)≤2.

  • 第5题：

    设A、B、C为同阶矩阵，且C为非奇异矩阵，满足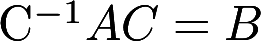，求证：


    答案：
    解析：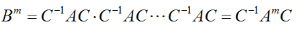

  • 第6题：

    证明：如果A是非奇异对称矩阵，则A^-1也是对称矩阵.


    答案：
    解析：

  • 第7题：

    设A为m×n矩阵，C是n阶可逆矩阵，矩阵A的秩为r1，矩阵B=AC的秩为r，则



    答案：C
    解析：

  • 第8题：

    矩阵A在（ ）时秩改变.

    A.转置
    B.初等变换
    C.乘以奇异矩阵
    D.乘以非奇异矩阵

    答案：C
    解析：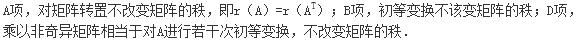

  • 第9题：

    MATLAB中符号矩阵的运算函数（）返回S矩阵的转置矩阵。

    • A、transpose（S）
    • B、determ（S）
    • C、colspace（S）
    • D、factor（S）

    正确答案:A

  • 第10题：

    填空题
    单元刚度矩阵具有对称性、（）性和奇异性。

    正确答案： 分块
    解析： 暂无解析

  • 第11题：

    多选题
    单元刚度矩阵和总体刚度矩阵都具有的共同特性为（）
    A

    对称性

    B

    分块性

    C

    正交性

    D

    奇异性

    E

    稀疏性


    正确答案： D,A
    解析： 暂无解析

  • 第12题：

    单选题
    如果视野将矩阵完全填充，且像素不是正方形，则像素的宽度等于（）
    A

    视野的宽度除以矩阵的行数

    B

    视野的高度除以矩阵的列数

    C

    视野的宽度除以矩阵的列数

    D

    视野的高度除以矩阵的行数

    E

    视野的高度乘以矩阵的行数


    正确答案： B
    解析： 如果视野将矩阵完全填充，像素宽度×矩阵列数=视野宽度；像素高度×矩阵行数=视野高度。

  • 第13题：

    下列选项中,不属于节点阻抗矩阵的性质的是()。

    A、对称性

    B、稀疏性

    C、可逆性

    D、非奇异性


    参考答案：B

  • 第14题：

    矩阵转置后,其行秩()。

    A.不变

    B.变大

    C.变小

    D.无法确定


    答案：A

    解析：以线性变换的角度理解矩阵，那么行列式代表“体积”的变化，秩代表像空间的维度。矩阵转置后行列式和秩不变；行和列是等价的，转置只是改变了行列的属性，而这两个属性没有什么意义，因此不会造成影响。

  • 第15题：

    设A为m阶实对称矩阵且正定，B为m×n实矩阵，B^T为B的转置矩阵，试证：B^TAB为正定矩阵的充分必要条件是B的秩r(B)=n，


    答案：
    解析：

  • 第16题：

    设A为n阶非奇异矩阵，α为n维列向量，b为常数.记分块矩阵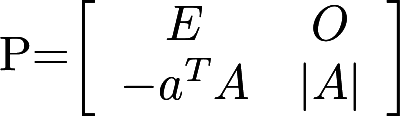.其中A*是矩阵A的伴随矩阵，E是n阶单位矩阵. （1）计算并化简PQ； （2）证明：矩阵Q可逆的充分必要条件是.


    答案：
    解析：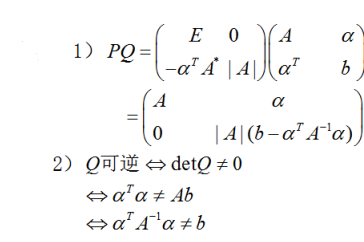

  • 第17题：

    设矩阵是4阶非零矩阵, 且满足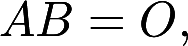证明矩阵B的秩


    答案：
    解析：

  • 第18题：

    矩阵A（ ）时可能改变其秩.《》（ ）

    A.转置：
    B.初等变换：
    C.乘以奇异矩阵：
    D.乘以非奇异矩阵.

    答案：C
    解析：

  • 第19题：

    设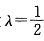是非奇异矩阵A的特征值，则矩阵（2A3）- 1有一个特征值为：

    A.3
    B.4
    C.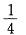
    D.1

    答案：B
    解析：
    提示：利用矩阵的特征值与矩阵的关系的重要结论：设λ为A的特征值，则矩阵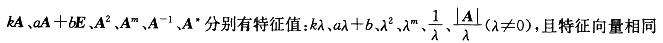

  • 第20题：

    单元刚度矩阵具有对称性、（）性和奇异性。


    正确答案:分块

  • 第21题：

    若格兰姆矩阵W（0，t1）为非奇异，则系统完全可控。


    正确答案:正确

  • 第22题：

    单选题
    矩阵A在（　　）时秩改变。
    A

    转置

    B

    初等变换

    C

    乘以奇异矩阵

    D

    乘以非奇异矩阵


    正确答案： C
    解析：
    A项，对矩阵转置不改变矩阵的秩，即r（A）＝r（AT）；
    B项，初等变换不该变矩阵的秩；
    D项，乘以非奇异矩阵相当于对A进行若干次初等变换，不改变矩阵的秩。

  • 第23题：

    单选题
    从左到右型HMM（即状态的转移只能从左到右或者停留在原状态，不能返回到以前的状态）的状态转移矩阵具有何种形式？（）
    A

    上三角矩阵；

    B

    下三角矩阵；

    C

    对称矩阵；

    D

    非奇异矩阵；


    正确答案： A
    解析： 暂无解析

  • 第24题：

    单选题
    MATLAB中符号矩阵的运算函数（）返回S矩阵的转置矩阵。
    A

    transpose（S）

    B

    determ（S）

    C

    colspace（S）

    D

    factor（S）


    正确答案： D
    解析： 暂无解析

相关内容