问答题证明：奇数阶反对称矩阵的行列式为零。

题目
问答题
证明：奇数阶反对称矩阵的行列式为零。
相似考题

1.若n阶矩阵A的秩为r,则____。A.A的行列式不等于0B.A的行列式等于0C.r>nD.r不大于n

2.设A,B为n阶对称矩阵,下列结论不正确的是().A.AB为对称矩阵 B.设A,B可逆,则A^-1+B^-1为对称矩阵 C.A+B为对称矩阵 D.kA为对称矩阵

3.设A，B为n阶矩阵，考虑以下命题：①若A，B为等价矩阵，则A，B的行向量组等价②若行列式.，则A，B为等价矩阵③若与都只有零解，则A，B为等价矩阵④若A，B为相似矩阵，则与的解空间的维数相同以上命题中正确的是（ ）. A.①③ B.②④ C.②③ D.③④

4.设A为n阶对称矩阵,则A是正定矩阵的充分必要条件是( ).A.二次型xTAx的负惯性指数零B.存在n阶矩阵C,使得A=CTCC.A没有负特征值D.A与单位矩阵合同

参考答案和解析
正确答案：
设A为n阶反对称矩阵,则AT=-A,因此,AT,=,-A,,即,A,=(-1)n,A,。当n为奇数时,有,A,=-,A,,则,A,=0。
解析： 暂无解析
更多“证明：奇数阶反对称矩阵的行列式为零。”相关问题

  • 第1题：

    下列结论中正确的是（　　）。

    A、 矩阵A的行秩与列秩可以不等
    B、 秩为r的矩阵中，所有r阶子式均不为零
    C、 若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零
    D、 秩为r的矩阵中，不存在等于零的r-1阶子式

    答案：C
    解析：
    A项，矩阵A的行秩与列秩一定相等。B项，由矩阵秩的定义可知，若矩阵A（m×n）中至少有一个r阶子式不等于零，且r＜min（m，n）时，A中所有的r+1阶子式全为零，则A的秩为r。即秩为r的矩阵中，至少有一个r阶子式不等于零，不必满足所有r阶子式均不为零。C项，矩阵A的行列式不等于零意味着矩阵A不满秩，n阶矩阵的秩为n时，所对应的行列式的值大于零；当n阶矩阵的秩＜n时，所对应的行列式的值等于零。D项，秩为r的矩阵中，有可能存在等于零的r-1阶子式，如秩为2的矩阵



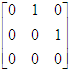
    中存在等于0的1阶子式。

  • 第2题：

    设A,B都是N阶对称矩阵，证明AB是对称矩阵的充分必要条件是.AB=BA


    答案：
    解析：

  • 第3题：

    设n阶实对称矩阵A的秩为r，且满足，求 ①二次型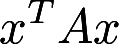的标准形； ②行列式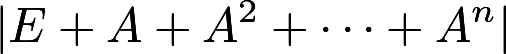的值，其中E为单位矩阵


    答案：
    解析：

  • 第4题：

    证明；对任意的n阶矩阵A，为对称矩阵，而为反对称矩阵.


    答案：
    解析：

  • 第5题：

    设A是n阶矩阵，E+A是可逆矩阵，记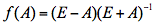，若A按足条件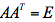，证明是反对称矩阵。


    答案：
    解析：


  • 第6题：

    设A=(aij)是三阶非零矩阵，｜A｜为A的行列式，Aij为aij的代数余子式，若aij+Aij=0(i，j=1，2，3)，则｜A｜=________.


    答案：1、-1.
    解析：

  • 第7题：

    设A是m阶矩阵，B是n阶矩阵，行列式等于（ ）。


    答案：D
    解析：

  • 第8题：

    当满足（）条件时，矩阵A为正定矩阵。

    • A、各阶顺序主子式均大于零
    • B、各阶顺序主子式均小于零
    • C、所有偶数阶主子式大于零
    • D、所有奇数阶主子式小于零

    正确答案:A

  • 第9题：

    问答题
    设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；

    正确答案： >>A=magic（4）
    >>B=inv（A）
    >>C=det（A）
    >>D=rank（A）
    >>E=trace（A）
    解析： 暂无解析

  • 第10题：

    问答题
    设n阶矩阵A有n个两两正交的特征向量，证明A是对称矩阵。

    正确答案：
    设A的n个两两正交的特征向量为α(→)1,α(→)2,…,α(→)n,其对应的特征值依次为λ1,λ2,…,λn。
    令ξ(→)i=α(→)i/,α(→)i,(i=1,2,…,n),则ξ(→)1,ξ(→)2,…,ξ(→)n是两两正交的单位向量。
    记P=(ξ(→)1,ξ(→)2,…,ξ(→)n),即P是正交矩阵。从而有P-1=PT,P-1AP=diag(λ1,λ2,…,λn)=Λ,即A=PΛP-1=PΛPT,故AT=(PΛPT)T=(PT)TΛTPT=PΛPT=A,即A是对称矩阵。
    解析： 暂无解析

  • 第11题：

    单选题
    若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。
    A

    正定

    B

    正定二次型

    C

    负定

    D

    负定二次型


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    下列结论中正确的是（    ）
    A

    矩阵A的行秩与列秩可以不等

    B

    秩为r的矩阵中，所有r阶子式均不为零

    C

    若n阶方阵A的秩小于n，则该矩阵A的行列式必等于零

    D

    秩为r的矩阵中，不存在等于零的r-1阶子式


    正确答案： D
    解析：

  • 第13题：

    设矩阵是4阶非零矩阵, 且满足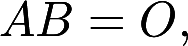证明矩阵B的秩


    答案：
    解析：

  • 第14题：

    设A为n阶对称矩阵，k为常数.试证kA仍为对称矩阵.


    答案：
    解析：

  • 第15题：

    已知n阶实对称矩阵Α≈B，证明:对于任何自然数k,


    答案：
    解析：

  • 第16题：

    设A为实对称矩阵,且A的特征值都大于零.证明：A为正定矩阵.


    答案：
    解析：

  • 第17题：

    设A为m×n阶实矩阵,且r(A)=n.证明：A^TA的特征值全大于零.


    答案：
    解析：

  • 第18题：

    下列命题正确的是（　　）。


    A.若三阶行列式Ｄ＝０，那么Ｄ中有两行元素相同
    B.若三阶行列式Ｄ＝０，那么Ｄ中有两行元素对应成比例
    C.若三阶行列式Ｄ中有６个元素为零，则Ｄ＝０
    D.若三阶行列式Ｄ中有７个元素为零，则Ｄ＝０

    答案：D
    解析：
    本题考查行列式的性质。

    若三阶行列式中Ｄ有７个元素为０，则它至少有一行或一列的元素全为０，即Ｄ＝０。

  • 第19题：

    设A为4阶魔术矩阵，分别对A进行如下操作： 求矩阵A的逆； 求矩阵A的行列式； 求矩阵A的秩； 求矩阵A的迹；


    正确答案: >>A=magic（4）
    >>B=inv（A）
    >>C=det（A）
    >>D=rank（A）
    >>E=trace（A）

  • 第20题：

    若矩阵A的所有奇数阶主子式小于零，而所有偶数阶主子式大于零，则该矩阵为（）矩阵。

    • A、正定
    • B、正定二次型
    • C、负定
    • D、负定二次型

    正确答案:C

  • 第21题：

    问答题
    设A＝[aij]3×3是三阶非零矩阵，而且满足aij＝－Aij（i，j＝1，2，3），其中Aij为行列式|A|中aij的代数余子式，求行列式|A|的值。

    正确答案：
    由题中条件可知A*=-AT,则,A*,=,-AT,。由,A*,=,A,3-1=,A,2,,-AT,=(-1)3,A,,则,A,2=(-1)3,A,=-,A,,故,A,=0或,A,=-1。
    因为矩阵A为非零矩阵,可设a11≠0,A的行列式为,A,=a11A11+a12A12+a13A13=-a112-a122-a132≠0,所以,A,=-1。
    解析： 暂无解析

  • 第22题：

    问答题
    证明：奇数阶反对称矩阵的行列式为零。

    正确答案：
    设A为n阶反对称矩阵,则AT=-A,因此,AT,=,-A,,即,A,=(-1)n,A,。当n为奇数时,有,A,=-,A,,则,A,=0。
    解析： 暂无解析

  • 第23题：

    单选题
    当满足（）条件时，矩阵A为正定矩阵。
    A

    各阶顺序主子式均大于零

    B

    各阶顺序主子式均小于零

    C

    所有偶数阶主子式大于零

    D

    所有奇数阶主子式小于零


    正确答案： B
    解析： 暂无解析

  • 第24题：

    单选题
    对于二阶行列式其结果等于（）的概率最大。
    A

    合数

    B

    素数

    C

    偶数

    D

    奇数


    正确答案： B
    解析： 暂无解析

相关内容