问答题求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

题目
问答题
求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。
相似考题

1.过点（2，1）且与直线y=0垂直的直线方程为 （ ）A.z=2B.x=1C.y=2D.y=1

2.直线L：(x-2)/1=(y-3)/2=(z-1)/1与平面Ⅱ：2x+y-4z=6的位置关系是( ).A.L垂直于Ⅱ B.L与Ⅱ相交，但不垂直 C.L与Ⅱ平行，且L不在Ⅱ上 D.L在Ⅱ上

3.已知直线L1过点M1(0，0，-1)且平行于X轴，L2过点M2(0，0，1)且垂直于XOZ平面，则到两直线等距离点的轨迹方程为( )。A. B. C. D.

4.设平面方程为x+y+z+1=0，直线方程为1－x=y+1=z，则直线与平面： A.平行 B.垂直 C.重合 D.相交但不垂直

参考答案和解析
正确答案：
过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
解析： 暂无解析
更多“求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝”相关问题

  • 第1题：

    过点(0，2，4)且与两平面x+2z=1和y-3z=2平行的直线方程是( ).

    A.x/0=(y-2)/1=(z-4)/(-3)
    B.x/1=(y-2)/0=(z-4)/2
    C.x/(-2)=(y-2)/(-3)=(z-4)/1
    D.x/(-2)=(y-2)/3=(z-4)/1

    答案：D
    解析：
    (1，0，2)×(0，1，-3)=(-2，3，1)=＞ D

  • 第2题：

    设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面：
    (A)平行 （B)垂直 (C)重合 (L)相交但不垂直


    答案：D
    解析：
    解：选D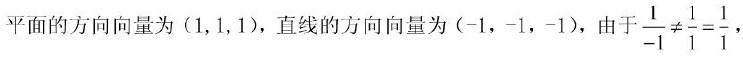
    所以直线与平面不垂直。又1x(-1) + 1x1+1x1=1≠0，所以直线与平面不平行。

  • 第3题：

    过点M(3，-2，1)且与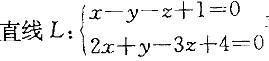平行的直线方程是：


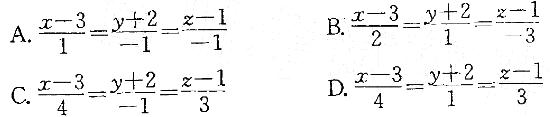    答案：D
    解析：
    提示:利用两向量的向量积求出直线L的方向向量。

  • 第4题：


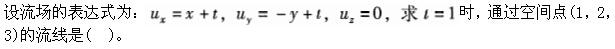    A.(x+1)(y+1)=2，z=3
    B.(x+1)(y-1)=2，z=3
    C.(x+1)(y-1)=-2，z=3
    D.(x+1)(y+1)=-2，z=3

    答案：B
    解析：

  • 第5题：

    过点P(2，-3)且在两坐标轴上截距相等的直线方程是( )

    A.χ+y+1=0或3χ+2y=0
    B.χ-y-1=0或3χ+2y=0
    C.χ+y-1=0或3χ+2y=0
    D.χ-y+1=0或3χ+2y=0

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为直线的截距． 【应试指导】若直线在两坐标轴上截距相等，将直线方程转化为截距式容易判别、选项A对．选项B错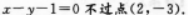，直线选项C错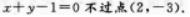，直线选项D错，直线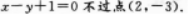

  • 第6题：

    已知平面π过点M1(1，1，0)，M2(0，0，1)，M3(0，1，1)，则与平面π垂直且过点(1，1，1)的直线的对称方程为：



    答案：A
    解析：
    提示 求出过M1，M2，M3三点平面的法线向量。



    @##

  • 第7题：

    已知直线／：ax+y=1在矩阵对应的变换作用下变为直线Z：x+by=l
    (1)求实数a，b的值；
    (2)若点P(x。，yo)在直线Z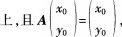求点P的坐标。


    答案：
    解析：
    (1）
    (2)

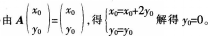
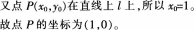
  • 第8题：

    已知两直线l1：x／2=（y+2）／-2=（1-x）／-1和l2：（x-1）／4=（y-3）／M=（z+1）／-2相互垂直，则M的值为：（）

    • A、3
    • B、5
    • C、-2
    • D、-4

    正确答案:B

  • 第9题：

    过点（-1，0，1）且与平面x+y+4z+19=0平行的平面方程为（）。

    • A、x+y+4z-3=0
    • B、2x+y+z-3=0
    • C、x+2y+z-19=0
    • D、x+2y+4z-9=0

    正确答案:A

  • 第10题：

    单选题
    已知两直线l1：x／2=（y+2）／-2=（1-x）／-1和l2：（x-1）／4=（y-3）／M=（z+1）／-2相互垂直，则M的值为：（）
    A

    3

    B

    5

    C

    -2

    D

    -4


    正确答案： A
    解析： 暂无解析

  • 第11题：

    单选题
    已知两直线l1：（x-4）／2=（y+1）／3=（z+2）／5和l2：（x+1）／-3=（y-1）／2=（z-3）／4，则它们的关系是（）
    A

    两条相交的直线

    B

    两条异面直线

    C

    两条平行但不重合的直线

    D

    两条重合的直线


    正确答案： B
    解析： 暂无解析

  • 第12题：

    单选题
    过点（-1，0，1）且与平面x+y+4z+19=0平行的平面方程为（）。
    A

    x+y+4z-3=0

    B

    2x+y+z-3=0

    C

    x+2y+z-19=0

    D

    x+2y+4z-9=0


    正确答案： C
    解析： 暂无解析

  • 第13题：

    过点（1，－2，3）且平行于z轴的直线的对称式方程是（　　）。



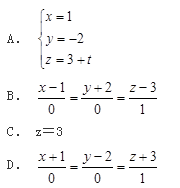    答案：B
    解析：
    由题意可得此直线的方向向量为（0，0，1），又过点（1，－2，3），所以该直线的方程为

  • 第14题：

    过点M(3，-2，1)且与直线L :平行的直线方程是：


    答案：D
    解析：
    直线L是平面χ - y- z +1 = 0和平面2χ+ y - 3z + 4 = 0的交线，直线L的方向向量

  • 第15题：

    设直线L过A(1，0，0)，B(0，1，1)两点，将L绕z轴旋转一周得到曲面∑，∑与平面z=0，z=2所围成的立体为Ω.
    　　(Ⅰ)求曲面∑的方程；
    　　(Ⅱ)求Ω的形心坐标.


    答案：
    解析：
    【分析】利用定义求旋转曲面∑的方程；利用三重积分求Ω的形心坐标.

  • 第16题：

    过点（2，0，－1）且垂直于xOy坐标面的直线方程是（　　）。


    答案：C
    解析：
    垂直于xOy面的直线的方向向量为（0，0，1），由于过点（2，0，－1），则直线的点向式方程为：（x－2）/0＝y/0＝（z＋1）/1。

  • 第17题：

    过点A(1,-1)，B(-1,1)且圆心在直线x+y-2=0上的圆的方程是（ ）。

    A.(x-3)2+(y+1)2=4
    B.(x+3)2+(y-1)2=4
    C.(x-1)2+(y-1)2=4
    D.(x+1)2+(y+1)2=4

    答案：C
    解析：

  • 第18题：

    试求通过点Mo(一1，0，4)，垂直于平面Ⅱ：3x一4y-10=0，且与直线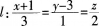
    平行的平面方程。


    答案：
    解析：
    平面Ⅱ的法向量m=（3-4，1)，直线Z的方向向量l=(3，l，2)，所以所求平面的法向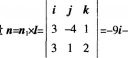

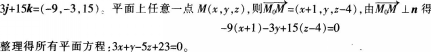
  • 第19题：

    求过点M（3,-2，1）且与直线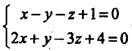平行的直线方程是（）。


    答案：D
    解析：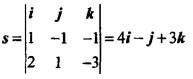
    *

  • 第20题：

    已知两直线l1：（x-4）／2=（y+1）／3=（z+2）／5和l2：（x+1）／-3=（y-1）／2=（z-3）／4，则它们的关系是（）

    • A、两条相交的直线
    • B、两条异面直线
    • C、两条平行但不重合的直线
    • D、两条重合的直线

    正确答案:B

  • 第21题：

    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.

    • A、（x-4）/2=（y+1）/0=（z-3）/5
    • B、（x-4）/2=（y+1）/1=（z-3）/5
    • C、（x+4）/2=（y-1）/0=（z+3）/5
    • D、（x+4）/2=（y-1）/1=（z+3）/5

    正确答案:B

  • 第22题：

    单选题
    过点（－1，2，3）垂直于直线x/4＝y/5＝z/6且平行于平面7x＋8y＋9z＋10＝0的直线是（　　）。
    A

    （x＋1）/1＝（y－2）/（－2）＝（z－3）/1

    B

    （x＋1）/1＝（y－2）/2＝（z－3）/2

    C

    （x＋1）/（－1）＝（y－2）/（－2）＝（z－3）/1

    D

    （x－1）/1＝（y－2）/（－2）＝（z－3）/1


    正确答案： A
    解析：
    直线x/4＝y/5＝z/6的方向向量为s＝4，5，6，平面7x＋8y＋9z＋10＝0的法向量为n＝7，8，9。显然ABC三项中的直线均过点（－1，2，3）。A项中直线的方向向量为s1＝（1，－2，1），有s1⊥s，s1⊥n，可见A中直线与已知直线x/4＝y/5＝z/6垂直，与平面7x＋8y＋9z＋10＝0平行。

  • 第23题：

    问答题
    求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

    正确答案：
    过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
    解析： 暂无解析

  • 第24题：

    单选题
    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.
    A

    （x-4）/2=（y+1）/0=（z-3）/5

    B

    （x-4）/2=（y+1）/1=（z-3）/5

    C

    （x+4）/2=（y-1）/0=（z+3）/5

    D

    （x+4）/2=（y-1）/1=（z+3）/5


    正确答案： A
    解析： 暂无解析

相关内容