单选题学校举行象棋比赛，共有甲、乙、丙、丁4支队。规定每支队都要和另外3支队各比赛一场，胜得3分，败得0分，平双方各得1分。已知：（1）这4支队三场比赛的总得分为4个连续的奇数；（2）乙队总得分排在第一；（3）丁队恰有两场同对方打成平局，其中有一场是与丙队打成平局的。问丙队得几分？（　　）A 1分B 3分C 5分D 7分

题目
单选题
学校举行象棋比赛，共有甲、乙、丙、丁4支队。规定每支队都要和另外3支队各比赛一场，胜得3分，败得0分，平双方各得1分。已知：（1）这4支队三场比赛的总得分为4个连续的奇数；（2）乙队总得分排在第一；（3）丁队恰有两场同对方打成平局，其中有一场是与丙队打成平局的。问丙队得几分？（　　）
A

1分

B

3分

C

5分

D

7分

相似考题

1.甲、乙、丙、丁比赛乒乓球，每两个人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同。问丁胜了几场？A．0B．1C．2D．3

2.某次棒球比赛共有甲、乙、丙、丁四队参加，每两队之间都要赛一场，已知乙队胜了丁队，且甲、乙、丙三队获胜的场次相同，那么丁队胜了( )场。A．3B．2C．1D．O

3.在冬奥会冰球比赛项目中,每支队伍有22人,双方上场各()人。A.6B.8C.10

4.：甲、乙、丙、丁四个人比赛乒乓球，每两人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同。问丁胜了几场?（ ）。 A．1B．2C．0D．3

更多“学校举行象棋比赛，共有甲、乙、丙、丁4支队。规定每支队都要和另外3支队各比赛一场，胜得3分，败得0分，平双方各得1分。已”相关问题

  • 第1题：

    一次象棋比赛共有10名选手参加，他们分别来自甲、乙、丙三个队，每个人都与其余九名选手各赛一盘，每盘棋的胜利者得1分，负者得0分，平局各得0.5分。结果甲队选手平均得4.5分，乙队选手平均得3.6分，丙队选手平均得9分，那么甲、乙、丙三队参加比赛的选手的人数依次是（ ）。

    A. 6人、3人、1人

    B.4人、5人、1人

    C. 3人、5人、2人

    D.5人、1人、4人


    正确答案：B

    B根据10名选手参加比赛，取胜者得1分，而丙队选手平均得分9分，这样丙队参赛选手只能是1人，且与其余9名选手比赛中应全部获胜。
    又根据每盘赛棋中胜者得1分，负者0分，平局各得0.5分，可知各队得分总数应是整数或小数部分的十位上是5，现乙队选手平均得3.6分，十位上是6，同样，甲、乙两队共有9人参赛，这样乙队参赛选手肯定是5人。
    因此甲队参赛选手人数是4人，乙队参赛选手人数是5人，丙队参赛选手人数是1人。

     

  • 第2题：

    甲，乙，丙，丁四人比赛乒乓球，规定每两人之间均要赛一场，结果甲胜丁，甲、乙、丙三人胜的场数相同，那么丁胜了多少场?

    A．3

    B．1

    C．0

    D．2


    正确答案：C
    [答案] C。解析：4人之间共有C42=6场比赛，一共会有6个胜利。如果甲只胜1场，乙和丙也只胜1场，那丁要胜6-3×1=3场，不合题意。所以只能是甲、乙、丙各胜2场，那么丁胜6-3×2=0场。选C。

  • 第3题：

    51．某单位五个科室间举办拔河比赛，每两个科室之间最多比赛一场。其中甲、乙、丙、丁科室分别参加了4、3、2和1场比赛，问已经进行了多少场比赛？

    A. 8
    B. 7
    C. 6
    D. 5

    答案：C
    解析：
    由题可知：甲与乙，甲与丙，甲与丁，甲与戊，乙与丙，乙与戊各打1场，共6场

  • 第4题：

    甲、乙、丙、丁四个人比赛乒乓球，每两人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同，问丁胜了几场?( )

    A. 1
    B. 2
    C. 0
    D. 3

    答案：C
    解析：
    四个人共有6场比赛，由于甲、乙、丙三人胜的场数相同，所以只有两种可能性：甲胜l场或甲胜2场。若甲只胜l场，这时乙、丙各胜1场，说明丁胜3场，这与甲胜丁矛盾，所以只可能是甲、乙、丙各胜2场，此时丁3场全败，也就是胜0场。故答案为C。

  • 第5题：

    在某届洲际杯足球大赛中，第一阶段某小组单循环赛共有4支队伍参加，每只队伍需要再这一阶段比赛三场。甲国足球队在该小组的前两轮比赛中一平一负。在第三轮比赛之前，甲国足球队教练在新闻发布会上表示："只有我们在下一场比赛中获得胜利并且本组的另外一场比赛打成平局，我们才有可能从这个小组出线。"

    A.甲国队第三场比赛取得了胜利，但他们未能从小组出线。
    B.第三轮比赛该小组另外一场比赛打成平局，甲国队从小组出线。
    C.第三轮比赛该小组两场比赛都分出了胜负，甲国队从小组出线。
    D.第三轮比赛甲国队取得了胜利，该小组另一场比赛打成平局，甲国队未能从小组出线。
    E.第三轮比赛该小组两场比赛都打成了平局，甲国队未能从小组出线

    答案：A
    解析：

  • 第6题：

    在某次大学生足球比赛中，有8支队伍在4个学校中进行循环赛，那么平均每个学校需要举行比赛（　　）场。

    A.4
    B.5
    C.6
    D.7

    答案：D
    解析：

  • 第7题：

    已知：（1）若甲和乙都参加比赛，则丙不能参加比赛。（2）只有乙参加比赛，丁才参加比赛。（3）甲和丙都参加了比赛。若以上判断都是真的，可否定乙和丁是否参加了比赛？写出推理过程。


    正确答案: 由题目得知如下三个判断：
    ①、甲并且乙则非丙；②、只有乙，才丁；③、甲，并且丙；由此可作如下推理：（1）假设乙参加比赛，而根据判断③甲也参加比赛，按判断①可得出丙没有参加比赛，结论与判断③矛盾，可见，乙参加比赛不能成立。（2）由于乙没参加比赛，据判断②，则乙也不可能参加比赛，所以，乙和丁都没参加比赛。

  • 第8题：

    问答题
    已知：（1）若甲和乙都参加比赛，则丙不能参加比赛。（2）只有乙参加比赛，丁才参加比赛。（3）甲和丙都参加了比赛。若以上判断都是真的，可否定乙和丁是否参加了比赛？写出推理过程。

    正确答案： 由题目得知如下三个判断：
    ①、甲并且乙则非丙；②、只有乙，才丁；③、甲，并且丙；由此可作如下推理：（1）假设乙参加比赛，而根据判断③甲也参加比赛，按判断①可得出丙没有参加比赛，结论与判断③矛盾，可见，乙参加比赛不能成立。（2）由于乙没参加比赛，据判断②，则乙也不可能参加比赛，所以，乙和丁都没参加比赛。
    解析： 暂无解析

  • 第9题：

    单选题
    学校举行象棋比赛，共有甲、乙、丙、丁4支队。规定每支队都要和另外3支队各比赛一场，胜得3分，败得0分，平双方各得1分。已知：（1）这4支队三场比赛的总得分为4个连续的奇数；（2）乙队总得分排在第一；（3）丁队恰有两场同对方打成平局，其中有一场是与丙队打成平局的。问丙队得几分？（　　）
    A

    1分

    B

    3分

    C

    5分

    D

    7分


    正确答案： B
    解析：
    每支队均比赛3场，因此最高分不超过9分，又知总得分为4个连续的奇数，因此得分有3、5、7、9和1、3、5、7两种情况。若最高分为9分，那么排名第二的队最多赢现场得6分，不可能得7分，不符合题意，故乙队得7分，即2胜1平。由条件（3）知，丁队恰有两场同对方打成平局，积分2分，为偶数，故另一场只能为胜，共得5分。由此可知，丙队得分为1或3分。由于丁队一场未败，故乙队获胜的两场只能是甲队和丙队。目前已知丙队战两场，一负一平，积1分，另一场无论是胜或平，积分均为偶数，故这一场只能为负，总积分为1分。

  • 第10题：

    问答题
    1994年“世界杯”足球赛中，甲、乙、丙、丁4支队分在同一小组。在小组赛中，这4支队中的每支队都要与另3支队比赛一场。根据规定：每场比赛获胜的队可得3分；失败的队得0分；如果双方踢平，两队各得1分。已知： （1）这4支队三场比赛的总得分为4个连续奇数； （2）乙队总得分排在第一； （3）丁队恰有两场同对方踢平，其中有一场是与丙队踢平的。 根据以上条件可以推断：总得分排在第四的是哪队？

    正确答案：
    解：（1）这4个连续奇数必为1，3，5，7，如果不是，只有3，5，7，9可能，这样第一名得9分（三场全胜），第二名最多得6分（胜两场），而不是7分。矛盾。所以，乙队得7分，而且一定是“2胜1平”。或者由每场双方得分之和最多3分，最少2分，所以，4支队共比6场，6场的总分A满足。
    12≤A≤18
    但是当4个奇数为3、5、7、9时，A=24，不在上面的范围内，所以，4个奇数为1、3、5、7。
    （2）由于丁队有两场踢平（已得2分），另一场必胜（得3分）。不然的话就是败，总分2分与“奇数”的条件矛盾。所以，丁队“2平1胜”，得5分。
    （3）由于丁队一场未败，所以，败给乙队的一定是甲队与丙队。
    （4）丙队不可能排第三（得3分）。这是因为它与乙、丁两队比的两场是“1平1败”，得1分，而把甲队打胜打平都不可能得2分。
    所以，丙队一定排在第四。
    答案是“丙”。
    解析： 暂无解析

  • 第11题：

    甲、乙、丙、丁、戊5支排球队进行单循环比赛(每两队间都只进行一场比赛)，比赛结果为：丁队只输了一场，丙队比丁队多赢一场，戊队比丁队多输一场，甲队比戊队多输两场，那么乙队的名次是(25)。

    A．第一名

    B．第三名

    C．第四名

    D．第五名


    正确答案：C
    解析：本题主要考查的是简单的逻辑思维能力。根据甲、乙、丙、丁、戊5支排球队进行单循环比赛得出每支球队都进行4场比赛，丁队只输一场，丙队比丁队多赢一场，那么丙队为第一名，丁队为第二名。戊队比丁队多输一场，则可以得出戊队为第三名，甲队比戊队多输两场可以得出甲队为第五名，因此乙队的名次只可能是第四名。

  • 第12题：

    甲乙丙丁四人参加象棋比赛，根据比赛规定每两人之间要比试一次，胜者计2分，平者计1分，负者计0分。已知全部比赛结束后，只出现了1次平局，且甲获得4分，乙获得3分，丙获得0分，丁获得5分。
    则下列陈述不正确的是：

    A.甲胜过了乙
    B.乙胜过了丁
    C.丁胜过了甲
    D.乙获得一胜一平一负

    答案：B
    解析：
    第一步，确定题型。
    题干有信息匹配特征，确定为分析推理。
    第二步，分析条件，进行推理。
    由“甲、乙、丙、丁每两人之间要比试一次”则每人均进行了3次比赛；
    由“只有1局平局”，根据胜负情况，可得出：甲胜2场，负1场；乙胜1场，平局1场，负1场；丙负3场，丁胜2场，平局1场。因此乙和丁是平局，B项不正确；
    乙与丁平一场，胜丙一场，因此，乙负的1场是负于甲，A、D项均正确，；
    丁共胜2场，与乙平1场，胜甲1场，胜丙1场，C项正确；

  • 第13题：

    甲乙丙丁戊五支足球队比赛，每两支队伍之间都要比赛-场， 到目前为止，乙队比赛了4场，丙队比赛了3场，丁队比赛了2场，戊队比赛了1场，那么甲队还要跟谁比赛?()


    A.丙戊
    B.丁戊
    C.丙丁
    D.乙丁

    答案：B
    解析：
    采用画图连线法，乙与甲、丙、丁、戊进行比赛，丙与乙、甲、丁进行了比赛，丁与乙、丙进行了比赛，戊与乙进行比赛，故甲还需要与丁、戊进行比赛。

  • 第14题：

    一项足球比赛共有8支队伍参加，每两支队伍之间需要踢两场比赛，获胜得3分，打平得1分，落败不得分。在该项足球比赛中，获得第一名的队伍积分最多可能比第二名多（ ）分。

    A.40
    B.30
    C.20
    D.10

    答案：B
    解析：
    第一步，本题考查趣味杂题中的比赛问题。?第二步，8支队伍参加，每两支队伍之间要踢2场比赛，一共需要进行



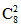
    ×2＝56场比赛，其中获得第一名的队伍，参加了14场比赛，最多得分为14×3＝42（分）（即14场比赛全部获胜），要想使第一名比第二名多的分数尽可能大，则要使第二名获得的分数尽可能少，每场比赛分出胜负两队共得3分，打成平局共得2分，所以尽量让其他场次都是平局，第一名参加14场，剩余56－14＝42（场），每场都是平局共得42×2＝84（分），剩下的7支队伍平均分配，每队12分。第三步，获得第一名的队伍积分比第二名最多多得42－12＝30（分）。因此，选择B选项。

  • 第15题：

    已知甲、乙、丙、丁、戊五人进行比赛，要求两两进行比赛，截止到某时刻，甲已比赛4场，乙比赛3场，丙比赛2场，戊比赛1场，则丁已比赛（）场。

    A.1
    B.2
    C.3
    D.4

    答案：B
    解析：
    根据题意，每人都要比赛4场，甲已赛4场，说明甲已与其他四人都赛过一场，由戌比赛1场可知是与甲进行的比赛；乙比赛3场，包括与甲赛过的一场，则乙必须与丙丁各赛1场；丙赛2场即与甲乙各赛1场，所以丁与甲乙各赛1场，共比赛2场。故本题答案为B。

  • 第16题：

    有4支队伍参加区小学生篮球比赛决赛，如果进行淘汰赛，最后决出冠军，共需比赛（）场。

    • A、6
    • B、4
    • C、3

    正确答案:C

  • 第17题：

    体育馆内正进行一场乒乓球双打比赛，观众议论双方运动员甲、乙、丙、丁的年龄： (1)“乙比甲的年龄大。” (2)“甲比他的伙伴的年龄大。” (3)“丙比他的两个对手的年龄都大。” (4)“甲与乙的年龄差距比丙与乙的年龄差距更大些。” 根据这些议论，甲、乙、丙、丁的年龄从大到小的顺序是( )。

    • A、甲、丙、乙、丁
    • B、丙、乙、甲、丁
    • C、乙、甲、丁、丙
    • D、乙、丙、甲、丁

    正确答案:D

  • 第18题：

    单选题
    有4支队伍参加区小学生篮球比赛决赛，如果进行淘汰赛，最后决出冠军，共需比赛()场。
    A

    6

    B

    4

    C

    3


    正确答案： B
    解析： 暂无解析

  • 第19题：

    单选题
    甲市乙区消防大队与丙市丁区消防大队发生管辖争议，后经指定丁区消防大队管辖。该项指定应当由下列哪一机关作出？（）。
    A

    甲市公安消防支队

    B

    乙市公安消防支队

    C

    甲市公安消防支队或乙市公安消防支队

    D

    甲市公安消防支队和乙市公安消防支队的共同上一级机关


    正确答案： D
    解析： 暂无解析

相关内容