单选题一张边长为2米的正方形纸张，对折3次后得到的小长方形的面积为（　　）平方米。A 0.2B 0.25C 0.5D 1

题目
单选题
一张边长为2米的正方形纸张，对折3次后得到的小长方形的面积为（　　）平方米。
A

0.2

B

0.25

C

0.5

D

1

相似考题

1.把一张长方形白纸连续对折2次，然后用针在上面扎出“田”字，展开后，共可得到多少个“田”字？

2.：一张面积为2平方米的长方形纸张，对折三次后得到的小长方形的面积是：A．12m2 B.13m2 C.14m2 D.18m2

3.长方形截面细长压杆,b／h=1／2;如果将长方形截面改成边长为h的正方形,后仍为细长杆,临界力Pcr是原来的()倍A、2B、4C、8D、16

4.一张边长为2米的正方形纸张，对折3次后得到的小长方形的面积为（ ）平方米。A．0.2B．O.25C．0.5D．1

更多“一张边长为2米的正方形纸张，对折3次后得到的小长方形的面积为（　　）平方米。”相关问题

  • 第1题：

    把一个正方形的一边减少2cm，另一边增加20%，得到一个长方形，它与原来的正方形面积相等，那么，正方形的边长是( )。m。

    A．13

    B．10

    C．12

    D．15


    正确答案：C
    C【解析】设正方形边长为xcm，依题得（x-2）×z(1+2%) =x2 得x=12cm。

  • 第2题：

    一张面积为2平方米的长方形纸张，对折3次后得到的小长方形的面积是（ ）。

    A．1/2m2

    B．1/3m2

    C．1/4m2

    D．1/8m2


    正确答案：C

  • 第3题：

    在下图中，大正方形的边长为10,连接大正方形的各边中点得到小正方形，将小正方 形每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分面积是（）。



    答案：C
    解析：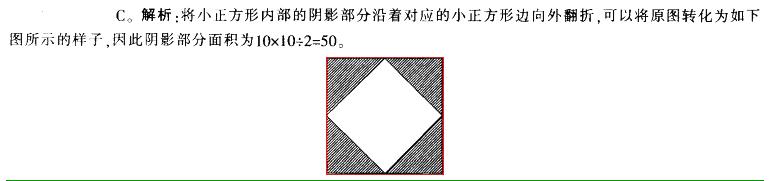

  • 第4题：

    如图所示，一个边长为16厘米的大正方形，在距离角一定位置处与对角线平行折叠四次，得到中部小正方形的边长为4厘米。如果CB与大正方形的对边平行，则三角形ABC的面积为（ ）。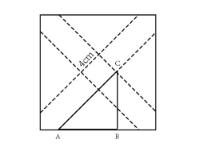

    A.32
    B.16
    C.16
    D.24

    答案：A
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，如下图所示，由于正方形的对角线互相垂直且平分，过正方形的中心做平行于底边的一条线，容易看出这条线过C点（否则小正方形对角线将不能垂直平分）。可知BC长度为正方形边长的一半，即16÷2=8厘米。由中心是小正方形，则∠ABC是直角的一半即45°，可知△ABC是一个等腰直角三角形，面积为8×8÷2=32（平方厘米）。

  • 第5题：

    市民广场中有两块草坪，其中一块草坪是正方形，面积为400平方米，另一块草坪是圆形，其直径比正方形边长长10%，圆形草坪的面积是多少平方米


    A.410
    B.400
    C.390
    D.380

    答案：D
    解析：
    正方形的边长是20米，那么圆的半径是20×1.1÷2=11米，那么圆形草坪的面积是3.14×11×11=379.9≈380。

  • 第6题：

    用全部156个边长为1的小正方形，最多可以拼成（ ）种形状不同的长方形。

    A.5
    B.6
    C.7
    D.8

    答案：B
    解析：
    第一步，本题考查约数倍数问题。
    第二步，小正方形总面积为156×1×1＝156，拼成不同形状的长方形，即枚举不同的长与宽，且满足长×宽＝156，将156进行因式分解，共有以下六种情况：1×156、2×78、3×52、4×39、6×26、12×13，最多可以拼成6种不同的长方形。
    因此，选择B选项。

  • 第7题：

    一正方形铁片面积为1平方米，用其剪出一个最大的圆，然后再圆中剪出一个最大的正方形，问新正方形的面积比原正方形的面积小多少？

    A.1/4平方米
    B.1/2平方米
    C.π/8平方米
    D.π/16平方米

    答案：B
    解析：
    第一步，本题考查几何问题，属于平面几何类。
    第二步，由正方形铁片面积为1平方米，可知正方形的边长是1米，切割出的新正方形的对角线为最大圆的直径，即原正方形的边长。新正方形的边长为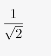


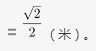
    新正方形的面积为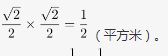

    第三步，故新正方形的面积比原正方形小了

  • 第8题：

    正方形边长为口，围成圆柱，体积为( )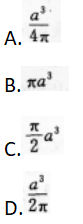


    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为圆柱的体积． 【应试指导】欲求圆柱的体积，由体积公式可知，必须知道圆柱的高(即正方形的边长)、半径，半径可由圆柱的周长等于正方形的边长求出。如图，

  • 第9题：

    某长方形长和宽的比是4:3，如果长减少4米，宽增加6米则变成一个正方形，原长方形的面积为（__）平方米？

    A. 900
    B. 1200
    C. 1500
    D. 1800

    答案：B
    解析：
    本题考查基础几何问题。设长为4x，宽为3x，4x-4=3x+6，解得x=10，则长方形长40，宽30，面积为30*40=1200

  • 第10题：

    一张A1大小的纸张经过两次对折，其大小为（）

    • A、A0
    • B、A2
    • C、A3
    • D、A4

    正确答案:C

  • 第11题：

    一张长方形纸，长2703厘米，宽1113厘米，要把它截成若干个同样大小的正方形，纸张不能有剩余且正方形的边长要尽可能大。问：这样的正方形的边长是多少厘米（）

    • A、153
    • B、156
    • C、158
    • D、159

    正确答案:D

  • 第12题：

    单选题
    一张边长为2米的正方形纸张，对折3次后得到的小长方形的面积为（　　）平方米。
    A

    0.2

    B

    0.25

    C

    0.5

    D

    1


    正确答案： B
    解析：
    正方形纸张的面积为2×2＝4平方米，每次对折后面积变为原来的1/2，经过3次折叠后，得到的长方形的面积为：4×（1/8）＝0.5平方米。

  • 第13题：

    给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。

    A．13

    B．26

    C．40

    B D．46


    正确答案：B

  • 第14题：

    下图中，每个小正方形网格都是边长为1的小正方形，则阴影部分面积最大是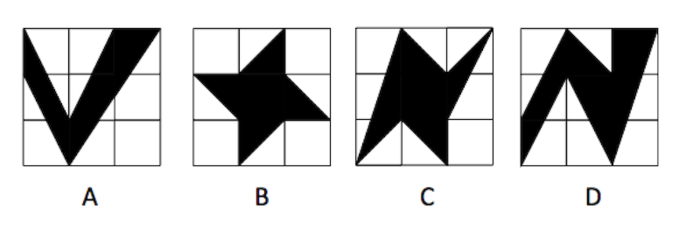： AA
    BB
    CC
    DD


    答案：D
    解析：
    解析:
    根据题目所给图形，可计算得：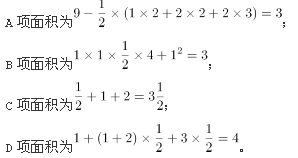

    故正确答案为D。

  • 第15题：

    在下图中，大正方形的边长为10，连接大正方形的各边中点得到小正方形，将小正方形 每边三等分，再将三等分点与正方形的中心和对应的顶点相连，得到如下图形。那么阴影部分 面积是（）。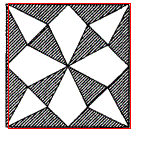


    A.25
    B.100/3
    C.50
    D.75

    答案：C
    解析：
    将小正方形内部的阴影部分沿着对应的小正方形边向外翻折，可以将原图转化为如下 图所示的样子，因此阴影部分面积为10x10+2=50。

  • 第16题：

    如下图所示，一张边长8厘米的正方形纸片先进行对折，再沿着两边的中点连线减掉一个角后，则剩下部分展开面积是多少平方厘米？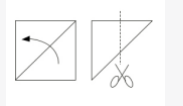

    A.16
    B.32
    C.36
    D.48

    答案：D
    解析：

  • 第17题：

    一张面积为48平方厘米的长方形铁皮，对折5次后得到铁皮的面积是多少平方里面?()

    A.1.5
    B.3
    C.0.75
    D.6

    答案：A
    解析：
    长方形对折5次之后面积变为原来的(1/2) 5=1/32， 故现在的面积为48*1/32=1.5

  • 第18题：

    如图，将正方形边长三等分后可得9个边长相等的小正方形，把中间的小正方形去掉，对剩下的8个小正方形，均按上面方法操作。问：对一个边长为2的正方形如此操作三次后所剩白色区域的面积是多少？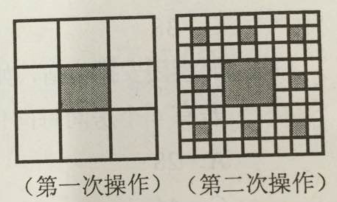

    A.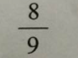
    B.
    C.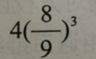
    D.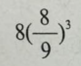

    答案：C
    解析：

  • 第19题：

    给长方形的长增加2，宽增加5恰好可以得到一个面积为100的正方形，则原长方形的周长( )。

    A. 13
    B. 26
    C. 40
    D. 46

    答案：B
    解析：
    故答案为B。

  • 第20题：

    用边长为120cm的正方形铁皮做一个无盖水箱，先在四角分别截去一个边长相等的小正方形，然后把四边垂直折起焊接而成，问剪去的小正方形的边长为多少时，水箱容积最大最大容积是多少


    答案：
    解析：
    设剪去的小正方形边长为x(cm)，则水箱底边长为120-2x，则水箱容积为

    ∴剪去的小正方形边长为20cm时水箱容积最大为128000cm3．

  • 第21题：

    一张面积为2平方米的长方形纸张，对折3次后得到的小长方形的面积是：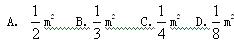


    答案：C
    解析：
    “对折n次”以及“折n折”。

  • 第22题：

    实地量得某一正方形水池面积为30.8025平方米，则在1：500的地形图上其边长为（）

    • A、30.8025米
    • B、5.55米
    • C、5.55厘米
    • D、1.11厘米

    正确答案:D

  • 第23题：

    用20个边长为1厘米的小正方形，能拼成（）个不同的长方形。

    • A、3
    • B、4
    • C、5

    正确答案:A

  • 第24题：

    单选题
    用20个边长为1厘米的小正方形，能拼成()个不同的长方形。
    A

    3

    B

    4

    C

    5


    正确答案： B
    解析： 暂无解析

相关内容