单选题某商店出售的一种商品，每天卖出1000件，每件可获利40元，现在他们采用提高售价、减少进货量的方法增加利润。根据经验，这种商品每涨价10元，每天就少卖出100件。若以每10元为一个提价单位，那么提价后，每天的最大利润是多少元？（　　）A 49000B 39000C 42000D 41000

题目
单选题
某商店出售的一种商品，每天卖出1000件，每件可获利40元，现在他们采用提高售价、减少进货量的方法增加利润。根据经验，这种商品每涨价10元，每天就少卖出100件。若以每10元为一个提价单位，那么提价后，每天的最大利润是多少元？（　　）
A

49000

B

39000

C

42000

D

41000

相似考题

1.某商店销售一批同型号的电风扇，按高于进价的20%的价格定销售价，预计获利9000元。由于其中20台电风扇的外皮有些损伤，这20台按销售价打八五折出售，因此最后获利只有预计获利的94%。这批电风扇共有多少台?A．280B．300C．320D．355

2.第13题：某商品每件成本72元，原来按定价出售，每天可卖10件，每天利润为成本的25%;后来按定价的90%出售，每天销售提高到原来的2.5倍，照这样计算，每天的利润比原来增加（ ）元。 A．500B．450C．400D．350

3.将进货单价为90元的某商品按100元一个出售，能卖出500个，已知这种商品如果每个涨价1元，其销售量就会减少10个，为了获得最大利润，售价应定为( )。A.110元/个B.120元/个C.130元/个D.150元/个

4.某商店拟放弃现在经营的商品A，改为经营商品B，有关的数据资料如下：（1）A的年销售量3600件，进货单价60元，售价100元，单位储存成本5元，一次订货成本250元。（2）B的预计年销售量4000件，进货单价500元，售价540元，单位储存成本10元，一次订货成本288元。（3）该商店按经济订货量进货，假设需求均匀、销售无季节性变化。（4）假设该商店投资所要求的报酬率为18%，不考虑所得税的影响。要求：（1）计算经营商品A和经营商品B各自的经济订货量。（2）计算分析该商店应否调整经营的品种（提示：不考虑经济订货量占用资金的机会成本）。

参考答案和解析
正确答案： C
解析：
设每件商品提价10x元，则每件商品获利（10x＋40）元，每天卖出的商品数量为（1000－100x）件。设每天获利为y元，则y＝（10x＋40）（1000－100x）＝－1000（x－3）2＋49000。得x＝3时，y＝49000元，为最大值。
更多“某商店出售的一种商品，每天卖出1000件，每件可获利40元，现在他们采用提高售价、减少进货量的方法增加利润。根据经验，这”相关问题

  • 第1题：

    将进货单价为90元的某商品按l00元一个出售时，能卖出500个，已知这种商品如果每个涨价1元，其销量就会减少10个，为了获得最大利润，售价应定为( )。

    A．110元

    B．120元

    C．130元

    D．150元


    正确答案：B
    93．B[解析]直接代入方法，可知当定价为120元时，获得最大利润(120-90)X(500—200)=90000(元)，选B。

  • 第2题：

    某种商品每件的进价为30元，在某段时间内若以每件x元出售，可卖出（100-x）件，应如何定价才能使利润最大？


    解：设所获利润为w元，则有：

    W=（x-30）（100-x）

      =-x²+130x-3000

      =-（x-65）²+1225

    ∴当x=65时，利润最大，最大利润为1225元。


  • 第3题：

    将进货单价为90元的某商品按100元一个出售时，能卖出500 个，已知这种商品如果每个涨价 1 元，其销售量就会减少 10 个，为了获得最大利润，售价应定为（）。

    A. 110 元

    B. 130 元

    C. 120 元

    D.150 元


    正确答案：C
    【解析】设涨价x 元，此时利润为 y，则y=（100+x-90）× （500-10×x），该函数为二次函数，其最值可使用导数求得。当 x=20 时，利润最大。故正确答案为 C。

  • 第4题：

    某商品每件成本72元，原来按定价出售，每天可售出100件，每件利润为成本的25%，后来按定价的900A出售，每天销售量比原来增加1.5倍。照这样计算，每天的利润比原来增加（ ）元。

    A．12500

    B．4500 T--T

    C．450

    D．300


    正确答案：C
    每件利润为成本的25%，则原来定价为72×(1+25%)=90元，后来的定价为90×90%=81元，销量为100×(1+1.5)=250件，所以每天的利润比原来增加250×(81-72)-100×(90-72)=450元。故选C。

  • 第5题：

    一批商品，按25%的利润率定价，卖出80%后。打折出售，每件丽品依然可获利25元，所有商品都卖出后，共获利45000元，经计算发现，打折出售的商品所获利润仅占总利润的石1/9，问该商品销售后期打几折出售?


    正确答案：D

  • 第6题：

    3个商店某种商品的库存相同。甲商店每天进货10件，销售25件；乙商店每天进货5件，销售30件。20天后甲的库存正好是乙的2倍。已知丙商店每天销售这种商品50件，问每天至少要进货多少件，才能保证50天内这种商品不会断货？（ ）

    A.28
    B.32
    C.36
    D.40

    答案：C
    解析：
    第一步，本题考查基础应用题。
    第二步，甲商店每天净消耗25－10＝15（件）库存，乙商店每天净消耗库存30－5＝25（件），设原来3个商店的库存为x，则20天后甲库存x－15×20＝x－300（件），20天后乙库存x－25×20＝x－500（件）。有等量关系x－300＝2×（x－500），解得x＝700。
    第三步，第50天时，一共卖了50×50＝2500（件），故需再进货2500－700＝1800（件），平均每天需要进货1800÷50＝36（件）。

  • 第7题：

    某类商品按质量分为8个档次，最低档次商品每件可获利8元，每提高一个档次，则每件商品的利润增加2元。最低档次商品每天可产出60件，每提高一个档次，则日产量减少5件。若只生产其中某一档次的商品，则每天能获得的最大利润是（ ）元。

    A.620
    B.630
    C.640
    D.650

    答案：C
    解析：
    第一步，本题考查经济利润问题，属于最值优化类。
    第二步，设提升了n个档次，则利润变为（8＋2n）元，销量变为（60－5n）件。利润的表达式为（8＋2n）×（60－5n）=10（4＋n）×（12－n）=10（48+8n-n2），当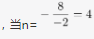

    时取最大值，即最大利润为10×8×8=640（元）。因此，选择C选项。

  • 第8题：

    一商店经销某种商品，每周进货的数量X与顾客对该种商品的需求量Y是相互独立的随机变量，且都服从区间［10，20］上的均匀分布.商店每售出一单位商品可得利润1000元；若需求量超过了进货量，商店可从其他商店调剂供应，这时每单位商品获利润为500元，试计算此商店经销该种商品每周所得利润的期望值.


    答案：
    解析：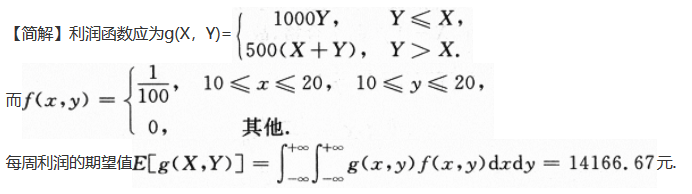

  • 第9题：

    某商店出售的一种商品，每天卖出1000件，每件可获利40元，现在他们采用提高售价、减少进货量的方法增加利润。根据经验，这种商品每涨价10元，每天就少卖出100件。若以每10元为一个提价单位，那么提价后，每天最大利润是多少元？（ ）
    A. 49000 B. 39000 C. 42000 D. 41000


    答案：A
    解析：
    设每件商品提价10x元，则每件商品获利（10x＋40）元，每天卖出的商品数量为（1000 －100x）件。设每天获利为y元，则
    y＝（10x＋40）（1OOO－1OOx）
    ＝ －1000x2＋6000x＋40000
    ＝ －1000[(x－3)2－49]
    ＝ －1000(x－3)2 ＋49000
    当x＝3时，y＝49000，为最大值。本题正确答案为A。

  • 第10题：

    某物业管理公司属下某商店本月购进A商品1000件，每件进价100元。本月出售A商品600件，每件售价150元。根据收入与支出配比原则，该商店本月销售毛利率为（）

    • A、100000元
    • B、10000元
    • C、30000元
    • D、90000元

    正确答案:C

  • 第11题：

    将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果在原售价的基础上每个涨价1元，其销售量就会减少10个，为了获得最大利润，售价应定为（）。

    • A、110元
    • B、120元
    • C、130元
    • D、150元

    正确答案:B

  • 第12题：

    单选题
    某商店出售的一种商品，每天卖出1000件，每件可获利40元，现在他们采用提高售价、减少进货量的方法增加利润。根据经验，这种商品每涨价10元，每天就少卖出100件。若以每10元为一个提价单位，那么提价后，每天的最大利润是多少元？（　　）
    A

    49000

    B

    39000

    C

    42000

    D

    41000


    正确答案： D
    解析：
    设每件商品提价10x元，则每件商品获利（10x＋40）元，每天卖出的商品数量为（1000－100x）件。设每天获利为y元，则y＝（10x＋40）（1000－100x）＝－1000（x－3）2＋49000。得x＝3时，y＝49000元，为最大值。

  • 第13题：

    某商店出售某种商品，可获利润35%，今以原售价的8折出售，问仍可获利百分之几？( )

    A.28

    B.15

    C.8

    D.7


    正确答案：C

  • 第14题：

    某商品每件成本72元，原来按定价出售，每天可卖10件，每天利润为成本的25%;后来按定价的90%出售，每天销售提高到原来的2.5倍，照这样计算，每天的利润比原来增加（ ）元。

    A．500

    B．450

    C．400

    D．350


    正确答案：B

  • 第15题：

    将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果每个涨价1元，其销量就会减少10个，为了获得最大利润，售价应定为( )。

    A.110元

    B.120元

    C.130元

    D.150元


    正确答案：A

  • 第16题：

    将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果每个涨价1元，其销售量就会减少10个，为了获得最大利润，售价应定为多少元?

    A．110

    B．120

    C．130

    D．150


    正确答案：B
    [答案] B。解析：设涨价x元，则所得利润为(100-90+x)×(500-10x)=-10(x-20)2+9000。当x=20时，利润最大，选B。

  • 第17题：

    某商店以每件6元的进价买回一批商品，售价为每件8. 4元，当卖了这批商品的3/4时，不仅收回了购买这批商品所付的款项，而且还获得利润90元，这批商品有（）。

    A.500件
    B.400件
    C.300件
    D.600件

    答案：C
    解析：
    设这批商品有X件，可列方程：6x=8.4X（3/4）X—90，解得x=300,所以本题答案为C。

  • 第18题：

    某商店出售某种商品，可获利润35%，今以原售价的8折出售，问仍可获利百分之几？

    A. 28
    B. 15
    C. 8
    D. 7

    答案：C
    解析：
    設定商品成本100,卖 135 現在卖 135*0.8= 108，故答案为C。

  • 第19题：

    某商店经销某种商品,每周进货数量X与顾客对该种商品的需求量Y之间是相互独立的,且都服从［10,20］上的均匀分布.商店每出售一单位商品可获利1000元；若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利500元,计算此商店经销该种商品每周所得利润的期望值.


    答案：
    解析：
    【解】设R为商店每周的利润，则有
    因为X，Y相互独立且都服从【10，20】上的均匀分布，所以(X，Y)的联合密度函数为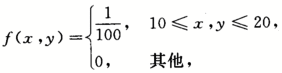

    故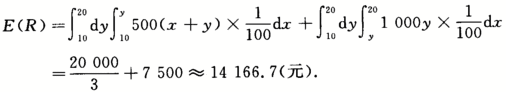

  • 第20题：

    一商店把某商品按标价的九折出售,仍可获利20%,若该商品的进价为每件21元,则该商品每件的标价为（ ）

    A.26元
    B.28元
    C.30元
    D.32元
    E.以上选项均不正确

    答案：B
    解析：
    设商品标价为x元,根据题意得0.9x-21=21×20%→x=28.

  • 第21题：

    商店购进一批衬衫，单价为80元，售价定为获利25%。但由于售价太高，几天过去后还有150件没卖出去，于是商店只得九折出售衬衫，又过了几天，商店经理统计了一下，一共卖出了180件，于是将最后的几件衬衫按进货价售出，最后商店一共获利2300元，求商店一共进了多少件衬衫？（ ）

    A. 100
    B. 200
    C. 300
    D. 400

    答案：B
    解析：
    经济利润问题。设商店一共进了件衬衫，以100元的价格卖了(-150)件，每件利润20元；以九折即90元的价格卖了180-(-150)=(330-)件，每件利润10元；最后的几件衬衫利润为0，因此总利润=20(-150)+10(330-)=2300，解得=200，因此本题选B。

  • 第22题：

    某商店以每件6元的进价买回一批商品，售价为每件8.4元，当卖了这批商品的3/4时，不仅收回了购买这批商品所付的款项，而且还获得利润90元，这批商品有（）。

    • A、500件
    • B、400件
    • C、300件
    • D、600件

    正确答案:C

  • 第23题：

    单选题
    某物业管理公司属下某商店本月购进A商品1000件，每件进价100元。本月出售A商品600件，每件售价150元。根据收入与支出配比原则，该商店本月销售毛利率为（）
    A

    100000元

    B

    10000元

    C

    30000元

    D

    90000元


    正确答案： A
    解析： 暂无解析

  • 第24题：

    单选题
    将进货单价为90元的某商品按100元一个出售时，能卖出500个，已知这种商品如果在原售价的基础上每个涨价1元，其销售量就会减少10个，为了获得最大利润，售价应定为（）。
    A

    110元

    B

    120元

    C

    130元

    D

    150元


    正确答案： B
    解析： 暂无解析

相关内容