单选题初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。A y－ln（1＋ey）＝x＋ln2B y＋ln（1＋ey）＝x－ln2C y＋ln（1＋ey）＝x＋ln2D y－ln（1＋ey）＝x－ln2

题目
单选题
初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。
A

y－ln（1＋ey）＝x＋ln2

B

y＋ln（1＋ey）＝x－ln2

C

y＋ln（1＋ey）＝x＋ln2

D

y－ln（1＋ey）＝x－ln2

相似考题

1.下面程序段中正确的是()。A.If x=2 Then y=3B下面程序段中正确的是( )。A．If x＜0 Then y=0 If x＜1 Then y=1 If x＜2 Then y=2 If x＞=2 Then y=3B．If x＞=2 Then y=3 If x＞1 Then y=2 If x＞=0Then y=1 If x＞0 Then y=0C．If x＜0 Then y=0 Else If＞=0Then y=1 Else y=3 End IfD．If x＞=2 Then y=3 Else If＞=1 Then y=2 Else y=0 End If

2.根据以下连环替代法的计算,可以计算因素b对Y的影响的是()Y0=a0×b0×c0Y1=a1×b0×c0Y2=a1×b1×c0Y3=a1×b1×c1。A、Y1-Y0B、Y2-Y1C、Y3-Y2D、Y3-Y1

3.设y是整形变量，能判断y为奇数的表达式是A．Not(y Mod 2＜＞0)B．y Mod 2＜＞0C．(y-1)Mod 2＜＞0D．y Mod 2＜＞1

4.直线z的方程为x-y-2=0，它关于点(1，-4)的对称直线方程为A．x+y-8=0B．x-y-8=0C．z+y+8=0D．x-y+8=0

参考答案和解析
正确答案： D
解析：
将微分方程y″＝e2y＋ey两边乘以2y′，得2y′y″＝（e2y＋ey）2y′，d（y′2）＝2（e2y＋ey）dy。两边积分得y′2＝2e2y＋ey＋C。将y（0）＝0，y′（0）＝2代入上式，得C＝1，故y′＝1＋ey，则有dy/（1＋ey）＝dx。积分可得y－ln（1＋ey）＝x＋C1，将y（0）＝0代入上式，得C1＝－ln2。故方程的解为y－ln（1＋ey）＝x－ln2
更多“初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。”相关问题

  • 第1题：

    设x=7,y=9,则以下表达式值为“真”的是A.x>=y And y>10B.x>y Or y>0C.x<0 Eqv y>0D.－2＋4>x And y>0

    设x=7，y=9，则以下表达式值为“真”的是

    A．x＞=y And y＞10

    B．x＞y Or y＞0

    C．x＜0 Eqv y＞0

    D．-2+4＞x And y＞0


    正确答案：B
    解析：在混合表达式中，按优先级有：先运算算术表达式，再运算比较表达式，最后运算逻辑表达式。选项B的运算结果为True。

  • 第2题：



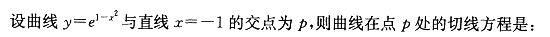    A.2x-y+2=0
    B.2x+y+1=0
    C.2x+y-3=0
    D.2x-y+3=0

    答案：D
    解析：
    提示：对y求导，代入x=-1得到切线斜率k=2，把x=-1代入曲线方程得交点（-1，1），利用点斜式写出切线方程。

  • 第3题：

    曲线y=x4-3在点(1，-2)处的切线方程为（）

    A.2x-y-6=0
    B.4x-y-6=0
    C.4x-y-2=0
    D.2x-y-4=0

    答案：B
    解析：
    【考情点拨】本题考查了曲线上一点处的切线方程的知识点．

  • 第4题：

    微分方程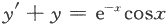满足条件y(0)=0的解为y=________.


    答案：
    解析：
    微分方程的通解为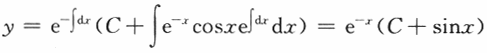.由初值条件y(0)=0得C=0.所以应填.

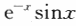
  • 第5题：

    曲线y=x3-4x+2在点(1，-l)处的切线方程为()

    A.x-y-2=0
    B.x-y=0
    C.x+y=0
    D.27+y-2=0

    答案：C
    解析：

  • 第6题：

    过直线3x＋2y＋1＝0与2x－3y＋5＝0的交点，且垂直于直线L：6x－2y＋5＝0的直线方程是（　　）

    A.x－3y－2＝0
    B.x＋3y－2＝0
    C.x－3y＋2＝0
    D.x＋3y＋2＝0

    答案：B
    解析：

  • 第7题：

    以为特解的二阶线性常系数齐次微分方程是（）。

    • A、y＂-2y＇-3y=0
    • B、y＂+2y＇-3y=0
    • C、y＂-3y＇+2y=0
    • D、y＂-2y＇-3y=0

    正确答案:B

  • 第8题：

    单选题
    初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。
    A

    y＋ln（1＋ey）＝x－ln2

    B

    y－ln（1＋ey）＝x－ln2

    C

    y－ln（1＋ey）＝x－2

    D

    y＋ln（1＋ey）＝x－2


    正确答案： B
    解析：
    将微分方程y″＝e2y＋ey两边乘以2y′，得2y′y″＝（e2y＋ey）2y′，d（y′2）＝2（e2y＋ey）dy。两边积分得y′2＝2e2y＋ey＋C。将y（0）＝0，y′（0）＝2代入上式，得C＝1，故y′＝1＋ey，则有dy/（1＋ey）＝dx。积分可得y－ln（1＋ey）＝x＋C1，将y（0）＝0代入上式，得C1＝－ln2。故方程的解为y－ln（1＋ey）＝x－ln2。

  • 第9题：

    单选题
    初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为（　　）。
    A

    y－ln（1＋ey）＝x＋ln2

    B

    y＋ln（1＋ey）＝x－ln2

    C

    y＋ln（1＋ey）＝x＋ln2

    D

    y－ln（1＋ey）＝x－ln2


    正确答案： C
    解析：
    将微分方程y″＝e2y＋ey两边乘以2y′，得2y′y″＝（e2y＋ey）2y′，d（y′2）＝2（e2y＋ey）dy。两边积分得y′2＝2e2y＋ey＋C。将y（0）＝0，y′（0）＝2代入上式，得C＝1，故y′＝1＋ey，则有dy/（1＋ey）＝dx。积分可得y－ln（1＋ey）＝x＋C1，将y（0）＝0代入上式，得C1＝－ln2。故方程的解为y－ln（1＋ey）＝x－ln2

  • 第10题：

    单选题
    设平面∏位于平面x－2y＋z－2＝0和平面x－2y＋z－6＝0之间，且将二平面间的距离分成1：3，则∏之方程为（　　）。
    A

    x－2y＋z－5＝0或x－2y＋z－3＝0

    B

    x＋2y＋z＋8＝0

    C

    x＋2y－4z＝0

    D

    x－2y＋z－8＝0


    正确答案： A
    解析：
    本题采用排除法较为简单。由于B、C两项所给出的平面方程的各项系数与已知平面不同，故它们与已知平面不平行，则可排除B、C项；D项平面与已知平面平行，但是不在两平面之间（可由常数项－8∉（－2，－6）判断出）。

  • 第11题：

    单选题
    过点（1，2）且与直线2x＋y－3＝0平行的直线方程为（　　）．
    A

    2x＋y－5＝0

    B

    2y－x－3＝0

    C

    2x＋y－4＝0

    D

    2x－y＝0


    正确答案： B
    解析：
    设和2x＋y－3＝0平行的直线方程为2x＋y＋c＝0，将（1，2）代人，则有2×1＋2＋c＝0，得c＝－4．

  • 第12题：

    填空题
    初值问题y″＝e2y＋ey，y（0）＝0，y′（0）＝2的解为____。

    正确答案： y-ln(1+ey)=x-ln2
    解析：
    将微分方程y″＝e2y＋ey两边乘以2y′，得2y′y″＝（e2y＋ey）2y′，d（y′2）＝2（e2y＋ey）dy。两边积分得y′2＝2e2y＋ey＋C。将y（0）＝0，y′（0）＝2代入上式，得C＝1，故y′＝1＋ey，则有dy/（1＋ey）＝dx。积分可得y－ln（1＋ey）＝x＋C1，将y（0）＝0代入上式，得C1＝－ln2。故方程的解为y－ln（1＋ey）＝x－ln2

  • 第13题：

    与y=(x>0?1:x<0?－1:0):的功能相同的if语句是()A.if(x>0)y=1; else if(x<0)y=－1; else y=0; else

    与y＝(x＞0?1:x＜0?-1:0)：的功能相同的if语句是( )

    A．if(x＞0)y=1； else if(x＜0)y=-1； else y＝0； else y=0；

    B．if(x) if(x＞0)y＝1； else if(x＜0)y=-1；

    C．y＝-1； if(x) if(x＞0)y＝1； else if(x==0)y＝0； else y=-1；

    D．y＝0； if(x＞=0) if(x＞0)y=1； else y=-1：


    正确答案：A

  • 第14题：

    以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：

    A. y"-2y'-3y=0
    B. y"+2y'-3y=0
    C. y"-3y'+2y=0
    D. y"+2y'+y=0

    答案：B
    解析：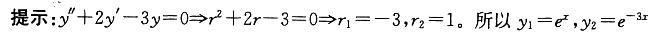
    B的特解，满足条件。

  • 第15题：

    若二阶常系数线性齐次微分方程y"+ay'+by=0的通解为y=(C1+C2x)e^x，则非齐次方程y"+ay'+by=x满足条件y(0)=2，y'(0)=0的解为y=________.


    答案：1、y=-xe^x+x+2.
    解析：

  • 第16题：

    过点P(2，-3)且在两坐标轴上截距相等的直线方程是( )

    A.χ+y+1=0或3χ+2y=0
    B.χ-y-1=0或3χ+2y=0
    C.χ+y-1=0或3χ+2y=0
    D.χ-y+1=0或3χ+2y=0

    答案：A
    解析：
    【考情点拨】本题主要考查的知识点为直线的截距． 【应试指导】若直线在两坐标轴上截距相等，将直线方程转化为截距式容易判别、选项A对．选项B错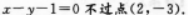，直线选项C错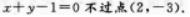，直线选项D错，直线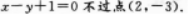

  • 第17题：


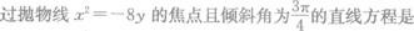    A.x＋y＋2＝0
    B.x－y＋2＝0
    C.x＋y－2＝0
    D.x－y－2＝0

    答案：A
    解析：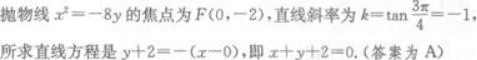

  • 第18题：

    曲线y=x3-4x+2在点(1，-1)处的切线方程为（　　）

    A.x-y-2-0
    B.x-y=0
    C.x+y=0
    D.x+y-2=0

    答案：C
    解析：

  • 第19题：

    填空题
    若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝____。

    正确答案： -xex+x+2
    解析：
    由题意可知，r＝1是已知齐次方程对应的特征方程的二重根，则该特征方程为（r－1）2＝r2－2r＋1＝0，齐次方程为y″－2y′＋y＝0设y*＝Ax＋B为已知非齐次方程y″－2y′＋y＝x的特解，代入y″－2y′＋y＝x得0－2A＋Ax＋B＝x，则A＝1，B＝2A＝2。故已知非齐次方程的通解为y＝（C1＋C2x）ex＋x＋2。又y（0）＝2，y′（0）＝0，代入以上通解得C1＝0，C2＝－1。故所求方程特解为y＝－xex＋x＋2。

  • 第20题：

    单选题
    若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝（　　）。
    A

    xex＋x2＋2

    B

    －xex＋x2＋2

    C

    －xex＋x＋2

    D

    －xex＋x


    正确答案： C
    解析：
    由题意可知，r＝1是已知齐次方程对应的特征方程的二重根，则该特征方程为（r－1）2＝r2－2r＋1＝0，齐次方程为y″－2y′＋y＝0设y*＝Ax＋B为已知非齐次方程y″－2y′＋y＝x的特解，代入y″－2y′＋y＝x得0－2A＋Ax＋B＝x，则A＝1，B＝2A＝2。故已知非齐次方程的通解为y＝（C1＋C2x）ex＋x＋2。又y（0）＝2，y′（0）＝0，代入以上通解得C1＝0，C2＝－1。故所求方程特解为y＝－xex＋x＋2。

  • 第21题：

    单选题
    （2012）以y1=ex，y2=e-3x为特解的二阶线性常系数齐次微分方程是：（）
    A

    y″-2y′-3y=0

    B

    y″+2y′-3y=0

    C

    y″-3y′+2y=0

    D

    y″+2y′+y=0


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    经过圆x2+2x+y2=0的圆心，与直线x+y=0垂直的直线方程是（）。
    A

    x+y+1=0

    B

    x-y-1=0

    C

    x+y-1=0

    D

    x-y+1=0


    正确答案： B
    解析： 圆x2+2x+y2=0的圆心是（-1，0），与直线x+y=0垂直的直线方程的斜率为1，可求得此直线方程为x-y+1=0。

  • 第23题：

    单选题
    悬臂梁长度为l，取自由端为坐标原点，则求梁的挠曲线时确定积分常数的边界条件为（）。
    A

    x=0、y=0；x=0、y¢=0

    B

    x=l、y=0；x=l、y¢=0

    C

    x=0、y=0；x=l、y¢=0

    D

    x=l、y=0；x=0、y¢=0


    正确答案： A
    解析： 暂无解析

  • 第24题：

    单选题
    若二阶常系数线性齐次微分方程y″＋ay′＋by＝0的通解为y＝（C1＋C2x）ex，则非齐次方程y″＋ay′＋by＝x满足条件y（0）＝2，y′（0）＝0的解为y＝（　　）。
    A

    xex＋x＋2

    B

    xex－x＋2

    C

    －xex－x＋2

    D

    －xex＋x＋2


    正确答案： C
    解析：
    由题意可知，r＝1是已知齐次方程对应的特征方程的二重根，则该特征方程为（r－1）2＝r2－2r＋1＝0，齐次方程为y″－2y′＋y＝0设y*＝Ax＋B为已知非齐次方程y″－2y′＋y＝x的特解，代入y″－2y′＋y＝x得0－2A＋Ax＋B＝x，则A＝1，B＝2A＝2。故已知非齐次方程的通解为y＝（C1＋C2x）ex＋x＋2。又y（0）＝2，y′（0）＝0，代入以上通解得C1＝0，C2＝－1。故所求方程特解为y＝－xex＋x＋2。

相关内容