单选题y=sin（1/x），当x接近于0时，函数图象的变化会（）。A 保持不变B 越来越慢C 越来越快D 以上答案均错误

题目
单选题
y=sin（1/x），当x接近于0时，函数图象的变化会（）。
A

保持不变

B

越来越慢

C

越来越快

D

以上答案均错误

相似考题

1.以下程序中，函数 fun 的功能是计算 x 2-2x+6 ，主函数中将调用 fun 函数计算：y1=(x+8) 2-2 (x+8)+6y2=sin 2(x)-2sin(x)+6请填空。#include "math.h"double fun(double x){ return (x*x-2*x+6); }main(){ double x,y1,y2;printf("Enter x:"); scanf("%lf",&x);y1=fun( 【 11 】 );y2=fun( 【 12 】 );printf("y1=%lf,y2=%lf\n",y1,y2);}

2.作出函数y=3-2x的图象，根据图象回答下列问题：（1）y的值随着x值增大而__________;（2）图象与x轴的交点坐标是_________________，与y轴的交点坐标是_______________；（3）当x__________时，y＞0 。

3.在同一直角坐标系内一次作出函数y=x+1，y=2x+1，y=3x+1的图象。（1）这几个图象之间有什么差别，又有什么联系？（2）一次函数y=kx+b的一次项系数k对函数的图象有什么影响？

4.以下程序中，函数fun的功能是计算x2-2x+6,主函数中将调用fun函数计算，请填空。y1=(x+8)2-2(x+8)+6y2=sin2(x)-2sin(x)+6 #include "math.h"double fun(double x){ return()；}main(){double x,y1,y2; printf("Enter x:"); scanf("%1f,&x); y1=fun(8+x); y2=fun()； printf("y1=%1f,y2=%1f\n",y1,y2);}

更多“y=sin（1/x），当x接近于0时，函数图象的变化会（）。”相关问题

  • 第1题：

    以下程序中，函数fun的功能是计算x2(上标)-2x＋6，主函数中将调用fun函数计算：

    y1=(x＋8)2(上标)-2(x＋8)＋6

    y2=sin2(上标)(x)-2sin(x)＋6

    请填空。

    include "math.h"

    double fun(double x){ return (x*x-2*x＋6);}

    main()

    { double x,y1,y2;

    printf("Enter x:"); scanf("%1f",&x);

    y1=fim([ ]);

    y2=run([ ]);

    printf("y1=%1f,y2=%1f\n",y1,y2);

    }


    正确答案：x＋8 sin(x)
    x＋8 sin(x) 解析：根据函数fun实现的功能可知：主函数中的y1、y2想要实现的是相同的功能，又根据　y1=(x＋8)2-2(x＋8)＋6=(x＋8)*(x＋8)-2(x＋8)＋6，可看出y1=fun(　　[11]　　)；处填：x＋8；同理可知y2=fun(　　[12]　　)；处填sin(x)。

  • 第2题：

    已知函数 y=x²-4x+3。

    （1）画出函数的图象；

    （2）观察图象，当x取哪些值时，函数值为0？

  • 第3题：

    11 、点 A （ 2 ， y 1 ） 、 B （ 3 ， y 2 ）是二次函数 y=x 2- 2x+1 的图象上两点，则 y 1 与 y 2 的大小关

    系为 y 1 _________ y 2 （填 “ ＞ ” 、 “ ＜ ” 、 “ = ” ） ．


    正确答案：

    <

    考点：二次函数图象上点的坐标特征。

    分析：本题需先根据已知条件求出二次函数的图象的对称轴，再根据点A、B的横坐标的大小即可判断出y1与y2的大小关系．

    解答：解：∵二次函数y=x2﹣2x+1的图象的对称轴是x=1，

    在对称轴的右面y随x的增大而增大，

    ∵点A（2，y1）、B（3，y2）是二次函数y=x2﹣2x+1的图象上两点，

    23，

    ∴y1y2．

    故答案为：．

    点评：本题主要考查了二次函数图象上点的坐标特征，在解题时要能灵活应用二次函数的图象和性质以及点的坐标特征是本题的关键．

  • 第4题：

    设函数y=sin(2x+1)，则y"=_____．


    答案：
    解析：
    填-4sin(2x+1)．

  • 第5题：

    当a≠0时，函数y=ax+1与y=a/x在同一坐标中图象可能是（）。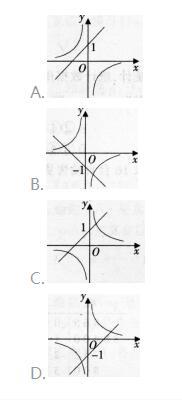


    答案：C
    解析：

  • 第6题：

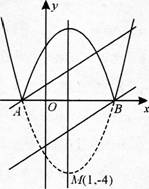
    下图是二次函数y=(x+m)2+k的图象，其顶点坐标为M(1，-4)．
    (1)求出图象与戈轴的交点A，B的坐标；



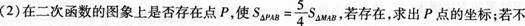
    存在，请说明理由；
    ° (3)将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b(b＜1)与此图象有两个公共点时，b的取值范围．





    答案：
    解析：
    解：(1)由二次函数Y=(x+m)2+k的顶点坐标为M(1，-4)可知，m=-1，k=-4.则二次函数Y=(x-1)2-4与x轴的交点为A(-1，0)，8(3，0).




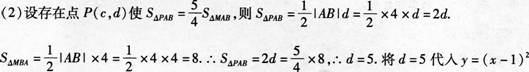
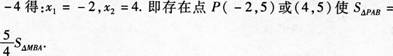
    (3)如图，当直线Y=x+b经过A(-1，0)时-1+b=0，
    可得b=1，又因为b＜1，
    故可知Y=x+b在Y=x+1的下方，
    当直线Y=x+b经过点B(3，0)时，3+b=0，则b=-3，
    由图可知，b的取值范围为-3＜b＜1时，
    直线Y=x+b(b＜1)与此图象有两个公共点.


  • 第7题：

    若函数y=(x)在[-1，1]上是单调函数，则使得y=(sinx)必为单调函数的区间是（ ）

    A.R
    B.[-1，1]
    C.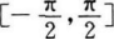
    D.[-sin1，sin1]


    答案：C
    解析：
    【考情点拨】本题主要考查的知识点为函数的单调区间． 1应试指导】y=(x)在[-1，1]上是单调函数，∴y=(x)的单调区间为[-1，1]，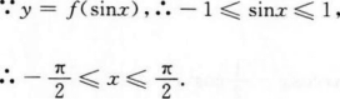

  • 第8题：

    函数y(x)的导函数f(x)的图象如图所示，Xo=-1，则( )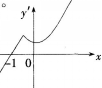

    A、X。不是驻点
    B、x。是驻点，但不是极值点
    C、x。是极小值点
    D、 X。极大值点

    答案：C
    解析：
    由图可知
    f，+(‰)>0，一(‰)<0且f(x)在x连续可导，故xo为极小值点。

  • 第9题：

    由函数y=ex的图象与y=-2x，x=1，x=3所围成的封闭面积为_______。


    答案：
    解析：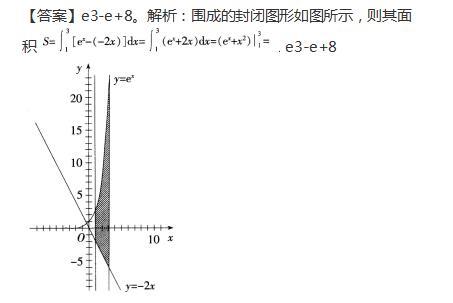

  • 第10题：

    已知函数f(x)=x2+4lnx．
    (1)求函数f(x)在[1，e]上的最大值和最小值；
    (2)证明：当x∈[1，+∞)时，函数八戈)的图象在g(x)=2x3的图象的下方。


    答案：
    解析：

  • 第11题：

    填空题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝____。

    正确答案： 1/sin2(sin1)
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第12题：

    单选题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。
    A

    1/sin2（sin1）

    B

    sin2（sin1）

    C

    －sin2（sin1）

    D

    －1/sin2（sin1）


    正确答案： B
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

  • 第13题：

    填空：

    （1）已知函数 y=2（x+1）²+1，当x＜____时，y随x的增大而减小，当x＞ _____时，y随x的增大而增大，当x=______时，y最_____；

    （2）已知函数 y=-2x²+x-4，当x＜_____时，y随x的增大而增大，当x＞_____时，y随x的增

    大而减小，当x=______时，y最_____；

    （3）二次函数 y=ax²+bx+c，a ＞0 ,当x＜_____时，y随x的增大而减小，当x＞_____时，y

    随x的增大而增大，当x=______时，y最_____；

    （4 )二次函数 y=ax²+bx+c，a ＜0 ,当x＜_____时，y随x的增大而增大，当x＞_____时，y随

    x的增大而减小，当x=______时，y最_____。


    (1)-1,-1,-1,小

    (2)1/4,1/4,1/4,大

    (3)-b/2a, -b/2a,-b/2a,小

    (4) -b/2a, -b/2a, -b/2a,大


  • 第14题：

    画出函数 y=x²-2x-3的图象，利用图象回答：

    （1）方程 x²-2x-3=0 的解是什么；

    （2）x取什么值时，函数值大于0 ；

    （3）x取什么值时，函数值小于0 。

  • 第15题：

    设函数y=sin2x，则y"=_____．


    答案：
    解析：
    填-4sin2x．y'=2cos2x．y＂=-4sin2x．

  • 第16题：


    A.常数k＜-1
    B.函数f(x)在定义域范围内，y随着x的增大而减小
    C.若点C(-1，m)，点B(2，n)，在函数f(x)的图象上，则m＜n
    D.函数f(x)图象对称轴的直线方程是y=x

    答案：C
    解析：
    由图象可知常数k＞0，A项错误；当x＞0时，y随着x的增大而减小，当x＜0时，y随着x的增大而减小，B选项说法不严谨，错误；由反比例函数的公式可得，m=-k＜0，



    m＜n，C正确；函数f(x)图象对称轴有两条，y=x和y=-x，D错误。

  • 第17题：

    函数f(x)=2sin3x的图象按向量a平移后得到的图象与g(x)=2cos3x的图象重合,则向量a可以是

    A.(-π/2,0)
    B.(π/2,0)
    C.(-π/6,0)
    D.(π/6,0)

    答案：C
    解析：
    ∵sin3x与cos3x互为余函数,又两函数周期都缩小了3倍 ∴移动后需重合必须移动π/2/3=±π/6 (+为右移,-为左移)
    又∵D(π/6,0),使f(x)=-g(x),(cos3x在第二象限) ∴选C

  • 第18题：

    关于反比例函数y=2/x，下列说法不正确的是()。，

    A.点(-2，-1)在它的图象上
    B.它的图象在第一、三象限
    C.当x>0时，y随x增大而增大
    D.当x<0时，y随x增大而减小

    答案：C
    解析：
    当x>0时，y随x增大而减小。

  • 第19题：

    下列函数图象与y=f（x）的图象关于原点对称的是（　　）

    A.y=-f（x）
    B.y=f（-x）
    C.y=-f（-x）
    D.y=｜f（x）｜

    答案：C
    解析：

  • 第20题：

    关于二次函数y=2-(x+1)2的图象,下列说法正确的是( )。

    A.图象开口向上
    B.图象的对称轴为直线x=1
    C.图象有最低点
    D.图象的顶点坐标(-1，2)

    答案：D
    解析：
    由二次函数图象的性质可知，其开口方向向下，有最大值2，对称轴为x=-1，顶点坐标(-1，2)。二次函数y=a(x+h)2+k(α≠0)中，α决定了二次函数图象的开口方向，顶点坐标为(-h，k)。

  • 第21题：

    一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k<0；②a>0；③当x<3时，y1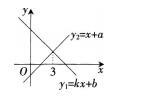

    A.0
    B.1
    C.2
    D.3

    答案：B
    解析：
    由一次函数y1=kx+b的图象可知，该函数在R上单调递减且与y轴的正半轴相交，由此可得k<0，b>0。同理，由一次函数y2=x+a的图象可知，该函数与y轴的负半轴相交，可得a<0。当x<3时，y1=kx+b的图象始终在，y2=x+a图象的上方，所以y1>y2。所以题中结论正确的只有①。

  • 第22题：

    已知函数 (x)=sin(ωx+φ)(ω>0)的图象如下图所示，则ω=（　　）。




    答案：B
    解析：

  • 第23题：

    单选题
    设f（x）是可导函数，且f′（x）＝sin2[sin（x＋1）]，f（0）＝4，f（x）的反函数是x＝φ（y），则φ′（4）＝（　　）。
    A

    sin2（sin1）

    B

    1/sin2（sin1）

    C

    sin（sin1）

    D

    1/sin（sin1）


    正确答案： D
    解析：
    φ′（4）＝1/f′（0）＝1/sin2（sin1）。

相关内容