单选题矩阵的乘法不满足哪一规律？（）A 结合律B 分配律C 交换律D 都不满足

题目
单选题
矩阵的乘法不满足哪一规律？（）
A

结合律

B

分配律

C

交换律

D

都不满足

相似考题

1.矩阵的乘法满足____。A.交换律B.分配律C.结合律

2.两个矩阵相乘,若矩阵总规模小于cache大小,则优化访存的最佳方法是____。A、先将两个矩阵读入cache再进行乘法B、先转置第一个矩阵再进行乘法C、先转置第二个矩阵再进行乘法D、以上皆错

3.在矩阵乘法的串行程序中,对____部分进行向量化收益最大。A、初始化B、第二个矩阵转置循环C、矩阵元素乘—加计算的循环D、结果输出

4.下列结论或等式正确的是()。A.若A，B均为零矩阵，则有A=BB.矩阵乘法满足交换律，则(AB)k=AkBkC.对角矩阵是对称矩阵D.若A≠0，B≠0，则AB≠0

更多“矩阵的乘法不满足哪一规律？（）”相关问题

  • 第1题：

    四元数是历史上第一次构造出的不满足乘法交换律的数系。()

    此题为判断题(对，错)。


    参考答案：正确。

  • 第2题：

    两个矩阵Am*n和Bn*p相乘，用基本的方法进行，则需要的乘法次数为m*n*p 多个矩阵相乘满足结合律，不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi,M{i+i)，…，Mj多个矩阵连乘的最优顺序，即所需要的乘法次数最少。最少乘法次数用m[i，j]表示，其递归式定义为：其中i、j和k为矩阵下标，矩阵序列中Mi的维度为(Pi-i.)*Pi采用自底向上的方法:实现该算法来确定n个矩阵相乘的顺序，其时间复杂度为( 64 )。若四个矩阵M1. M2、M3.，M4相乘的维度序列为2、6、3、10.3，采用上述算法求解，则乘法次数为( 65 )。

    A.O(N2)

    B.O(N2Lgn)

    C.O(N3)

    D.O(n3lgn)


    正确答案：C

  • 第3题：

    两个矩阵Am*n和Bn*p相乘，用基本的方法进行，则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律，不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi，M（i+1），…，Mj多个矩阵连乘的最优顺序，即所需要的乘法次数最少。最少乘法次数用m[i,j]表示，其递归式定义为：



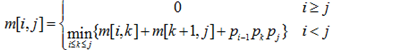
    其中i、j和k为矩阵下标，矩阵序列中Mi的维度为（pi-1）*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序，其时间复杂度为（ ）

    A.O（n2）
    B.O（n2lgn）
    C.O（n3）
    D.O（n3lgn）

    答案：C
    解析：
    四个矩阵分别为：
    2*6 6*3

  • 第4题：

    矩阵的乘法规则不满足传统的乘法交换律。


    正确答案:正确

  • 第5题：

    需求源于什么，哪一个不是（）

    • A、对现况的不满足
    • B、欲望不满足
    • C、生活的不满足
    • D、自我不满足

    正确答案:D

  • 第6题：

    矩阵的组合特性是矩阵乘法满足结合率，不满足交换率，即进行连续变换时一定要按变换次序对变换矩阵求积后才得到总的变换矩阵。


    正确答案:错误

  • 第7题：

    模糊评价结论是通过（）得出的。

    • A、归一化处理
    • B、矩阵加法
    • C、矩阵乘法
    • D、头脑风暴法

    正确答案:A

  • 第8题：

    矩阵的乘法不满足哪一规律？（）

    • A、结合律
    • B、分配律
    • C、交换律
    • D、都不满足

    正确答案:C

  • 第9题：

    判断题
    矩阵的组合特性是矩阵乘法满足结合率，不满足交换率，即进行连续变换时一定要按变换次序对变换矩阵求积后才得到总的变换矩阵。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第10题：

    单选题
    Strassen矩阵乘法是利用（）实现的算法。
    A

    分治策略

    B

    动态规划法

    C

    贪心法

    D

    回溯法


    正确答案： C
    解析： 暂无解析

  • 第11题：

    判断题
    在齐次坐标系中，若用矩阵来表示各种运算，则比例和旋转变换是矩阵乘法运算，而平移变换是矩阵加法运算。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第12题：

    判断题
    矩阵的乘法规则不满足传统的乘法交换律。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

  • 第13题：

    阐述矩阵乘法的运算过程。并用矩阵乘积形式表示如下线性方程组。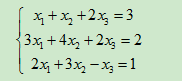

    用初等变换的方法求解上述线性方程组。


    答案：

  • 第14题：

    阅读下列说明和C代码，回答问题1至问题3

    【说明】 某工程计算中要完成多个矩阵相乘（链乘）的计算任务。 两个矩阵相乘要求第一个矩阵的列数等于第二个矩阵的行数，计算量主要由进行乘法运算的次数决定。采用标准的矩阵相乘算法，计算Am×n*Bn×p，需要m*n*p次乘法运算。 矩阵相乘满足结合律，多个矩阵相乘，不同的计算顺序会产生不同的计算量。以矩阵A110×100，A2100×5，A35×50三个矩阵相乘为例，若按（A1*A2）*A3计算，则需要进行10*100*5+10*5*50=7500次乘法运算；若按A1*（A2*A3）计算，则需要进行100*5*50+10*100*50=75000次乘法运算。可见不同的计算顺序对计算量有很大的影响。 矩阵链乘问题可描述为：给定n个矩阵


    答案：
    解析：

  • 第15题：

    两个矩阵Am*n和Bn*p相乘，用基本的方法进行，则需要的乘法次数为m*n*p。多个矩阵相乘满足结合律，不同的乘法顺序所需要的乘法次数不同。考虑采用动态规划方法确定Mi，M（i+1），…，Mj多个矩阵连乘的最优顺序，即所需要的乘法次数最少。最少乘法次数用m[i,j]表示，其递归式定义为：



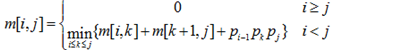
    其中i、j和k为矩阵下标，矩阵序列中Mi的维度为（pi-1）*pi采用自底向上的方法实现该算法来确定n个矩阵相乘的顺序，若四个矩阵M1、M2、M3、M4相乘的维度序列为2、6、3、10、3，采用上述算法求解，则乘法次数为（ ）。

    A.156
    B.144
    C.180
    D.360

    答案：B
    解析：
    四个矩阵分别为：
    2*6 6*3

  • 第16题：

    矩阵乘法有一个奇特的性质：不符合传统乘法的（）。

    • A、分配律
    • B、交换律
    • C、结合律
    • D、消去律

    正确答案:B

  • 第17题：

    在齐次坐标系中，若用矩阵来表示各种运算，则比例和旋转变换是矩阵乘法运算，而平移变换是矩阵加法运算。


    正确答案:错误

  • 第18题：

    Strassen矩阵乘法是利用（）实现的算法。

    • A、分治策略
    • B、动态规划法
    • C、贪心法
    • D、回溯法

    正确答案:A

  • 第19题：

    "吉芬商品"是不满足需求规律的例外。（）


    正确答案:正确

  • 第20题：

    矩阵乘法不满交换律也不满足结合律。


    正确答案:错误

  • 第21题：

    单选题
    模糊评价结论是通过（）得出的。
    A

    归一化处理

    B

    矩阵加法

    C

    矩阵乘法

    D

    头脑风暴法


    正确答案： A
    解析： 暂无解析

  • 第22题：

    多选题
    采用齐次坐标来实现图形变换的优点是（）
    A

    既可使矩阵变换满足结合率也可使矩阵变换满足交换率。

    B

    所有的图形变换都可以用矩阵乘法来实现。

    C

    可使矩阵变换满足结合率但不满足交换率。

    D

    可使非线性变换也能采用线性变换来实现。

    E

    可方便地实现任意的图形变换组合。

    F

    所有的图形变换都可以用矩阵加法来实现。


    正确答案： D,A
    解析： 暂无解析

  • 第23题：

    判断题
    矩阵乘法不满交换律也不满足结合律。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第24题：

    单选题
    矩阵的乘法不满足哪一规律？（）
    A

    结合律

    B

    分配律

    C

    交换律

    D

    都不满足


    正确答案： B
    解析： 暂无解析

相关内容