单选题一个数的0.01倍，积与原数比（）。A 大B 小C 无法比较
题目
大
小
无法比较
相似考题
更多“一个数的0.01倍，积与原数比（）。”相关问题
-
第1题：
：一个两位数，十位上的数字是个位上的数字的丁2，把十位上与个位上的数字调换后，新数比原数大18，则原来这个两位数的两个数字和是（ ）
A．12
B．10
C．8
D．21
正确答案：B满足十位数是个位数字的导的数只能是23，46和69，这三个两位数的两个数字之和分别是5，10和15，选项中只出现10，所以选择B。
-
第2题：
填空：
（1）一个数的平方等于它本身，这个数是___________；一个数的平方根等于它本身，这个数是______；一个数的算术平方根等于它本身，这个数是_____________。
（2）一个数的立方等于它本身，这个数是________________；一个数的立方根等于它本身，这个数是_______________。
（1）一个数的平方等于它本身，这个数是0和1；一个数的平方根等于它本身，这个数是0；一个数的算术平方根等于它本身，这个数是0和1。
（2）一个数的立方等于它本身，这个数是-1，0，1；一个数的立方根等于它本身，这个数是-1，0，1。
-
第3题：
一个两位数，十位上的数字是个位上的数字的2／3，把十位上与个位上的数字调换后，新数比原数大
18，则原来这个两位数的两个数字之和是( )。
A．12
B．10
C．8
D．2l
正确答案：B
-
第4题：
有五个连续偶数，已知第三个数比第一个数与第五个数之和的1/4多18，则这五个偶数之和是( )
A.210 B.180 C.150 D.100
正确答案：B
设五个偶数分别是al，a2，a3，a4，a5，因为五个偶数是连续的，所以，第三个是第一个与第五个的和的1/2，即a3=(1/2)(a1+a5)，又依题意，第三个数比第一个数与第五个数之和的1/4多18，所以a3=(1/4) (a1+a5)+18，即(1/2) (a1+a5)= (1/4)(a1+a5)+18，所以a1+a5=72，所以a3= 1/2×72=36，五个偶数的和是36x5=180。 -
第5题：
有五个连续偶数，已知第三个数比第一个数与第五个数之和的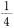
多18,则这五个偶数之和是（ ）。
A. 210 B. 180 C. 150 D. 100答案：B解析：
-
第6题：
五个连续奇数中，第三个数比第一个数与第五个数之和的1/3大9.那么，这五个奇数的和是多少? ( )
A.108
B.115
C.129
D.135答案：D解析：由于是连续的奇数， 故形成等差数列，按照前5项和的求和公式有[5*(a1+a5)]2=a3*5，解得a3=27,故前5项的和为5*27=135. -
第7题：
将1～9九个自然数分成三组，每组三个数，第一组三个数之积是48，第二组三个数之积是45，第三组数字中三个数之和最大是多少？（）
- A、15
- B、17
- C、18
- D、20
正确答案:C -
第8题：
几个数字相乘或相除时，所得的积或商的有效数字的保留位数，应以相对误差最大的那一个数为标准。（）
正确答案:正确 -
第9题：
一个数的0.01倍，积与原数比（）。
- A、大
- B、小
- C、无法比较
正确答案:B -
第10题：
一个数的2.3倍，积与原数比大
正确答案:错误 -
第11题：
单选题将1～9九个自然数分成三组，每组三个数，第一组三个数之积是48，第二组三个数之积是45，第三组数字中三个数之和最大是多少？（）A15
B17
C18
D20
正确答案： D解析： 45=1X5X9，分解唯一的，剩下2，3，4，6，7，8。因为第一组三个数之积为48，排除7、8两个数，当48=2×4X6时，剩下3，7，8，相加为3+7+8=18，满足条件。故选C。 -
第12题：
单选题一个数增加15%后得到一个新数，再从新数中减少15%，结果比原数相比（）A结果比原数大
B结果比原数小
C结果与原数相等
正确答案： B解析： 暂无解析 -
第13题：
有一串自然数，已知第一个数与第二个数互质，而且第一个数的5/6恰好是第二个数的1/4，从第三个数开始，每个数字正好是前两个数的和，问这串数的第2005个数被3除所得的余数是（ ）。
A．2
B．1
C．0
D．3
正确答案：C
第一个数的
等于第二个数的
，则可知第一个数与第二个数之比为3：10，由于这两个数互质，所以第一个数为3，第二个数为10，从而这串数为3，10，13，23，36，59，95，154，249，403，652，1055，…，这一数列被3除的余数是：0，1，1，2，0，2，2，1，0，1，1，2，…，按“0，1，1，2，0，2，2，1”循环。因为2005÷8＝250…5，所以第2005个数被3除所得的余数应该是第251个周期中的第5个数，即0。
-
第14题：
将1-9九个自然数分成三组，每组三个数，第一组三个数之积是48，第二组三个数之积是45，三组数字中数字之和最大是多少?
A．15
B．17
C．18
D．20
正确答案：C
[答案] C。解析：本题的突破口是45=1×5×9，在剩下的6个数当中，积为48的三个数可以是2×4×6或者2×3×8，当选择2×4×6时剩下的一组是3、7、8和为18，为最大。
-
第15题：
一个两位数，将个位数字与十位数字调换后，比原数小18，且这个原数是8的倍数，则这个数是多少?（ ）
A．24
B．32
C．40
D．64
正确答案：D
-
第16题：
下面说法正确的是( )。A.一个数的倒数一定比这个数大
B.边长为4 cm的正方形的周长面积相等
C.一个数除以分数的商一定比原来数大
D.若大牛和小牛的头数比是4：5，则大牛比小牛少1/5答案：D解析：
-
第17题：
数学运算。在这部分试题中．每道试题呈现一段表述数字关系的文字，要求你迅速、准确地计算出答案。
有五个连续偶数，已知第三个数比第一个数与第五个数之和的多18，则这五个偶数之和是（）。
A.210
B.180
C.150
D.100答案：B解析：设第一个数为x，由题意列方程：x+4=×(2x+8)+18，解得x=32。五个偶数之和为(32+32+8)×5÷2=180，选择B。
-
第18题：
一只密码箱的密码是一个三位数，满足3个数字之和为19，十位上的数比个位上的数大2。若将百位上的数与个位上的数对调，得到一个新密码，且新密码数比原密码的数大99，则原密码数是：A.397
B.586
C.675
D.964答案：B解析：第一步，本题考查多位数问题，用代入排除法解题。
第二步，根据十位上的数字比个位上的数字大2，发现四个选项都满足，根据百位上的数字与个位数字对调，新密码比原密码大99可得，只有B选项586对调后得到685，且685－586＝99满足题意。
因此，选择B选项。 -
第19题：
自然数的个数比偶数的个数（）。
- A、多
- B、少
- C、同样多
- D、不能判断
正确答案:C -
第20题：
一个数比B多2记作+2，那么另一数比B少7应记作（）。
- A、+7
- B、﹣7
- C、﹣5
- D、+5
正确答案:B -
第21题：
一个数增加15%后得到一个新数，再从新数中减少15%，结果比原数相比（）
- A、结果比原数大
- B、结果比原数小
- C、结果与原数相等
正确答案:B -
第22题：
判断题一个数的2.3倍，积与原数比大A对
B错
正确答案： 错解析： 暂无解析 -
第23题：
单选题一个数的0.01倍，积与原数比()。A大
B小
C无法比较
正确答案： C解析： 暂无解析 -
第24题：
单选题三个连续的奇数，后两数之积与前两数之积的差为2004，则这三个数中最小的数为多少（ ）A497
B499
C201
D203
正确答案： A解析：