已知正常人某定量指标的总体均值μ0=5,今随机测得某地一组特殊人群中的30人该指标的数值,为推断这组人群该指标的总体均值μ与μ0之间的差别是否有显著性意义,若用t检验,则自由度应该是()A、5B、28C、29D、4
题目
已知正常人某定量指标的总体均值μ0=5,今随机测得某地一组特殊人群中的30人该指标的数值,为推断这组人群该指标的总体均值μ与μ0之间的差别是否有显著性意义,若用t检验,则自由度应该是()
- A、5
- B、28
- C、29
- D、4
相似考题
更多“已知正常人某定量指标的总体均值μ0=5,今随机测得某地一组特殊人群中的30人该指标的数值,为推断这组人群该指标的总体均值μ与μ0之间的差别是否有显著性意义,若用t检验,则自由度应该是()A、5B、28C、29D、4”相关问题
-
第1题:
某总体含有n个个体,今测得n个个体某定量指标的数值,便可求得总体均值与总体标准差。计算总体标准差时,其自由度应该是
A、n-1
B、n
C、n-2
D、n+1
E、与n无关
参考答案:B
-
第2题:
为比较两种人群的血糖均值是否有差别,测得n =10,n
=10,n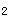 =10,
=10,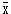
 =140,
=140,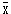
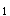 =120,S
=120,S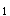 =15,S
=15,S =12,要推断其两总体均数是否有差别时,可应用A.两样本比较的秩和检验
=12,要推断其两总体均数是否有差别时,可应用A.两样本比较的秩和检验
B.t检验
C.配对资料符号秩和检验
D.u检验
E.χ 检验答案:B解析:
检验答案:B解析: -
第3题:
两个样本均值经过t检验判定有显著性差别,P值越小,则越有理由认为两总体均值有差别。
正确答案:正确 -
第4题:
设总体为正态总体,总体方差未知,在小样本条件下,对总体均值进行如下的假设检验H0:μ=μ0,(μ0为已知数);Hl:μ≠μ0,α=0.1。则下列说法正确的有()。
- A、(-∞,-z0.10)和(z0.10,+∞)为原假设的拒绝区域
- B、(-∞,-z0.05)和(z0.05,+∞)为原假设的拒绝区域
- C、(-∞,-t0.10)和(t0.10,+∞)为原假设的拒绝区域
- D、(-∞,-t0.05)和(t0.05,+∞)为原假设的拒绝区域
- E、若检验统计量的绝对值越大,则原假设越容易被拒绝
正确答案:D,E -
第5题:
平均值是描述数据集中程度的特征值。如果样本的均值有少许提高,则下列陈述正确的是()。
- A、总体均值提高
- B、总体均值不变
- C、总体均值下降
- D、尚不能确定总体均值是否有显著性变化
正确答案:D -
第6题:
一个总体有200个个体,且均值是180,方差是196。对该总体进行随机抽样,样本容量为49,总体的分布是未知的。则x-的均值和标准误差是()。
- A、180和24.39
- B、180和28
- C、180和2
- D、180和1.74
正确答案:D -
第7题:
某厂生产的产品厚度服从正态分布,厚度的均值为4。某天测得30产品样本的厚度的均值为3.89,欲检验与原来的均值相比是否有所变化,要求的显著性水平为0.05,则其假设形式是()。
- A、H0:μ=4;HA:μ≠4
- B、H0:μ=4;HA:μ>4
- C、H0:μ=4;HA:μ<4
- D、H0:μ≠4;HA:μ=4
正确答案:A -
第8题:
已知总体的均值为100,标准差为10,从该总体中随机抽取容量为100的样本,则样本均值抽样分布的标准误差为()
- A、100
- B、10
- C、1
- D、50
正确答案:C -
第9题:
单选题单样本t检验的原理是:若在总体平均数为μ0的假设总体中()抽到,判定()与μ0有差异。A能够,x均值
B能够,μ
C不能,x均值
D不能,μ
正确答案: C解析: 暂无解析 -
第10题:
单选题检验A与B的总体均值是否有差异的验证结果(显著性水平5%),得到P值为0.0019,对此解释正确的是()AA和B的总体均值相同
BA和B的总体均值不相同
CA和B的总体均值约有0.0019程度的差异
DP值太小,无法对A与B的总体均值下任何结论
正确答案: D解析: 暂无解析 -
第11题:
单选题检验A与B的总体均值是否有差异,在显著性水平5%验证的结果,得到P值为0.0019,对此解释正确的是()AA和B的总体均值相同
BA和B的总体均值不相同
CA和B的总体均值约有0.0019程度的差异
DP值太小,无法对A与B的总体均值下任何结论
正确答案: B解析: 暂无解析 -
第12题:
单选题某厂生产的产品厚度服从正态分布,厚度的均值为4。某天测得30产品样本的厚度的均值为3.89,欲检验与原来的均值相比是否有所变化,要求的显著性水平为0.05,则其假设形式是()。AH0:μ=4;HA:μ≠4
BH0:μ=4;HA:μ>4
CH0:μ=4;HA:μ<4
DH0:μ≠4;HA:μ=4
正确答案: C解析: 暂无解析 -
第13题:
用样本均值估计总体均值,在总体方差已知的情况下,应使用()。A:Z检验
B:T检验
C:F检验
D:R检验答案:A解析:一般来说,用样本均值估计总体均值,总体方差已知,用Z统计量检验;用样本均值估计总体均值,总体方差未知,用T统计量检验。 -
第14题:
如果要检验两个总体均值是否有显著差别,一般采用(),若要检验多个总体均值是否相等,则应该采用()。
正确答案:假设检验;方差分析 -
第15题:
已知某地正常人某定量指标的总体均值μ0=5,今随机测得该地特殊人群中的30人该指标的数值。若用t检验推断该特殊人群该指标的总体均值μ与μ0之间是否有差别,则自由度为()。
- A、5
- B、28
- C、29
- D、4
- E、30
正确答案:C -
第16题:
已知某地正常人某定量指标的总体均值μ0=5,今随机测得该地某人群中80人该指标的数值,若资料满足条件使用,检验来推断该人群该指标的总体均值μ与μ0之间是否有差别,则自由度为()
- A、4
- B、5
- C、76
- D、79
- E、80
正确答案:D -
第17题:
在描述数据集中程度的特征值中,均值是其中的一个。如果样本的均值有少许提高,则表明()。
- A、总体均值提高
- B、总体均值下降
- C、尚不能确定总体均值是否有显著性变化
- D、总体均值不变
正确答案:C -
第18题:
以下问题可以用Z检验的有()。
- A、正态总体均值的检验,方差已知
- B、正态总体均值的检验,方差未知
- C、大样本下总体均值的检验
- D、正态总体方差的检验
正确答案:A,C -
第19题:
某一指标的均值为3,方差为4,有一观测值为5,则标准化后其值为()
- A、1
- B、0.5
- C、-1
正确答案:A -
第20题:
单选题某总体含有n个个体,今测得n个个体某定量指标的数值,便可求得总体均值与总体标准差。计算总体标准差时,其自由度应该是An-1
Bn
Cn-2
Dn+1
E与n无关
正确答案: D解析: 暂无解析 -
第21题:
填空题如果要检验两个总体均值是否有显著差别,一般采用(),若要检验多个总体均值是否相等,则应该采用()。正确答案: 假设检验,方差分析解析: 暂无解析 -
第22题:
判断题两个样本均值经过t检验判定有显著性差别,P值越小,则越有理由认为两总体均值有差别。A对
B错
正确答案: 错解析: 暂无解析 -
第23题:
单选题某总体含有n个个体,现测得n个个体某定量指标的数值,即可求得总体均数值与总体标准差,计算总体标准差时,其自由度应该是()。An-1
Bn
Cn-2
Dn+1
En+2
正确答案: E解析: 暂无解析
