两个相互独立的随机变量的联合自信息量等于（）。

第1题：

两个相互独立的随机变量X与Y的标准差分别为Var (X) =2和Vaa (Y) = 1，则其差的标准差σ(X-Y)=( )。

答案：C

解析：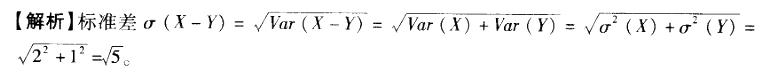

第2题：

下列关于两个相互独立的随机变量X1和X2的标准差和方差表达式，正确的是（ ）。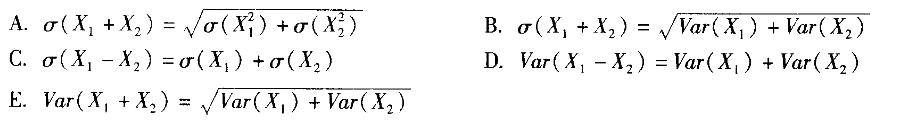

答案：B,D

解析：

X1和X2相互独立时，有：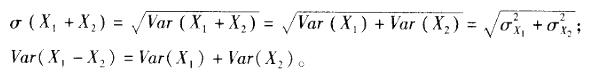

第3题：

设随机变量X与Y相互独立,下表列出二维随机变量(X,Y)的联合分布律及关于X和Y的边缘分布律的部分数值,试将其余的数值填入表中空白处.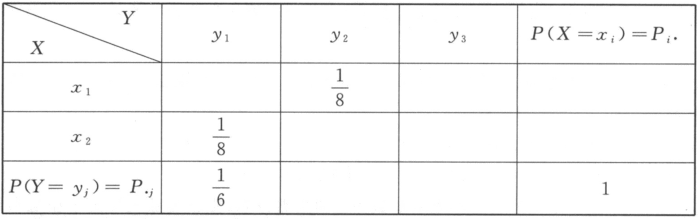

答案：

解析：

第4题：

设随机变量X和Y相互独立，下表列出了二维随机变量(X，Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值.试将其余数值填入表中的空白处.
　　

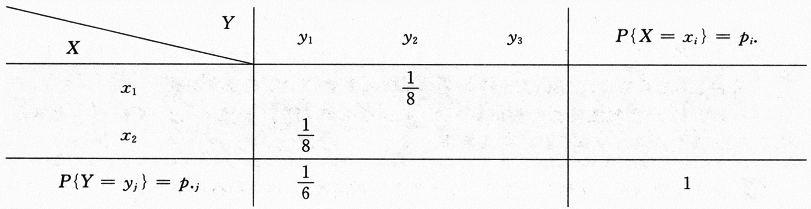答案：

解析：

当离散型随机变量(X，Y)中X与Y相互独立时，有进一步就有，也就是说(X，Y)的分布律中，当X，Y独立就对应各行成比例.有了这一点再加上边缘分布性质，就能很快解得

第5题：

若随机变量X与Y相互独立，且X在区间[0,2]上服从均匀分布，Y服从参数为3的指数分布，则数学期望E(XY)等于：

答案：D

解析：

提示X与Y独立时，E(XY)=E(X)E(Y)，X在[a，b]上服从均匀分布时，E(X) =

第6题：

答案：D

解析：

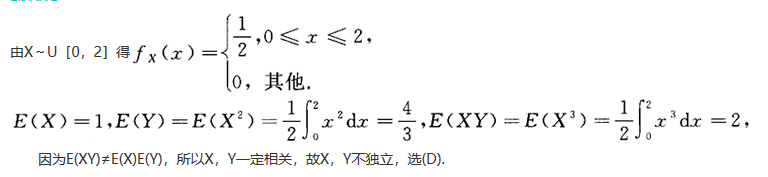
第7题：

答案：A

解析：

第8题：

若两个随机变量X，Y相互独立，则它们的连续函数g（X）和h（Y）所确定的随机变量（）.

• A、不一定相互独立
• B、一定不独立
• C、也是相互独立
• D、绝大多数情况下相独立

第9题：

如果随机变量X和Y服从联合正态分布，且X与Y的协方差为0，则X与Y相互独立。

第10题：

第11题：

第12题：

第13题：

设X与Y为相互独立的随机变量，且Var(A)=4, Var(Y) =9,则随机变量的标准差为（ ）。

答案：D

解析：

Var(Z) =Var(2X-Y) =4Var(X) + Var( Y) =4x4+9= 25，则随机变量Z=2X - Y的标准差为: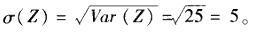

第14题：

设二维随机变量(X,Y)的联合密度函数为f(x,y)=
　　(1)求随机变量X,Y的边缘密度函数；
　　(2)判断随机变量X,Y是否相互独立；
　　(3)求随机变量Z=X+2Y的分布函数和密度函数.

答案：

解析：

第15题：

设随机变量X,Y独立同分布,且P(X=i)=,i=1,2,3.
　　设随机变量U=max{X,Y},V=min{X,Y}.
　　(1)求二维随机变量(U,V)的联合分布；(2)求Z=UV的分布；
　　(3)判断U,V是否相互独立？(4)求P（U=V）.

答案：

解析：

第16题：

第17题：

设随机变量X,Y相互独立,X～U(0,2),Y～E(1),则.P(X+Y>1)等于().

答案：A

解析：

第18题：

第19题：

设两个相互独立的随机变量X和Y分别服从正态分布N(0，1)和N(1，1)，则

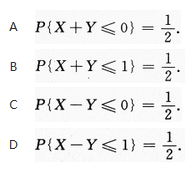答案：B

解析：

【简解】首先应看到，X+Y和X-Y均为一维正态分布的随机变量.其次要看到，如果z～N(μ，σ^2)，则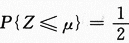，反之，如果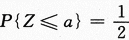，则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化，更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解，就更复杂化了.

第20题：

设两个相互独立的随机变量X和Y的方差分别为4和2，则随机变量3X-2Y的方差是（）

• A、8
• B、16
• C、28
• D、44

第21题：

如果两个随机变量不相关，则这两个随机变量一定相互独立。

第22题：

第23题：