有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚。求笼中各有几只鸡和兔？（）A、鸡有23只，兔有12只B、鸡有12只，兔有23只C、鸡有20只，兔有15只D、鸡有15只，兔有20只

题目

有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚。求笼中各有几只鸡和兔？（）

  • A、鸡有23只，兔有12只
  • B、鸡有12只，兔有23只
  • C、鸡有20只，兔有15只
  • D、鸡有15只，兔有20只
相似考题

1.第 14 题 有一列数，第一个数为8，第二个数为4，从第二个数起，它们的每个数都比它前后相邻的两数的和少5，从第一个数到第2003个数的和是（　　）。A．10001B．10000C．10011D．11000

2.鸡兔同笼，共有30个头，88只脚。求笼中鸡兔各有多少只？

3.有关“确定表元的数据来源于报表系统自身取数”叙述正确的有()A.从同一表页的不同单元取数B.从系统中其他报表取数C.从同一报表的不同表页取数D.从其他会计软件取数

4.在下面括号里填上适当的数。7/10=14/()=()/30 3/4=()/8=9/()8/24=2/()=()/3 5/9=()/18=15/()

更多“有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有9”相关问题

  • 第1题：

    某商场有7箱饼干，每箱装的包数相同，如果从每箱里拿出25包饼干，那么，7个箱里剩下的饼干包数相当于原来的2箱饼干，原来每箱饼干有多少包？（ ）。

    A．25 B．30 C．50 D．35


    正确答案：D

  • 第2题：

    蜘蛛有8条腿，蜻蜓有6条腿。现有蜘蛛、蜻蜓若干只，她们共有120条腿，且蜻蜓的只数是蜘蛛的2倍。蜘蛛、蜻蜓各有多少只？


    解：设蜘蛛有x只，蜻蜓有2x只，由题意得8x+6×2x=120，20x=120，x=6，2x=12

    答：蜘蛛有6只，蜻蜓有12只。

  • 第3题：

    一个农民有若干鸡和兔子,它们共有50个头和140只脚,那么兔子有多少只()。

    A、10

    B、20

    C、30

    D、40


    正确答案:B

  • 第4题：

    有红、黄、绿三种颜色的手套各6双，装在一个黑色布袋里，从袋子里任意取出手套来，为确保至少有2双手套不同颜色，则至少要取出的手套只数是（ ）。 A．15只 B．13只 C．12只 D．10只


    正确答案：A
    假设最先取了12只同一颜色的手套，要确保至少有2双手套不同颜色，则要再取3只手套，最少一共要取15只手套。故选A。

  • 第5题：

    在一个大笼子里关了一些鸡和一些兔子。数它们的头，一共有36个；数它们的腿一共有100条。问鸡和兔各多少只？（ ）


    正确答案：C

  • 第6题：

    有一个笼子里关着若干只兔子和鸡，鸡和兔子的数量之和与鸡腿和兔子腿之和的比是 2∶5。问鸡和兔子的数量之比是（）。

    A. 1∶3 B. 3∶1 C. 2∶3 D. 3∶2


    正确答案：B

    笼子中，平均每两只动物有5条腿。也就是说，平均每4只动物有10只腿。用简单的试凑法可以知道，1只兔子和3只鸡恰好是10只腿。所以鸡和兔子的数量比为3∶1。

  • 第7题：

    有一个笼子里关着若干只兔子和鸡．鸡和兔子的数量之和与鸡腿和兔子腿之和的比是2：5。问鸡和兔子的数量之比是（）[农行真题]
    A.1：3
    B.3：1
    C.2：3
    D.3：2


    答案：B
    解析：
    鸡和兔子的数量之和与鸡腿和兔子腿之和的比是2：5，设笼子里关的都是鸡，且鸡的数量为2x，则鸡腿的数量为4x，兔子的数量=(5x-4x)÷2=。鸡和兔子的数量之比是(2x-)：=3：1。选择B。

  • 第8题：

    从1,2,…,9这九个数中,随机抽取3个不同的数,这3个数的和为偶数的取法有（ ）种

    A.36
    B.44
    C.60
    D.72
    E.90

    答案：B
    解析：

  • 第9题：

    “鸡兔同笼”是我国民间流传的诗歌形式的数学题，“鸡兔同笼不知数，三十六头笼中露，看来脚有100只，几只鸡儿几只兔 ”解决此问题，设鸡为x只，兔为y只，所列方程组正确的是（　　）.


    答案：A
    解析：

  • 第10题：

    数据结构与算法里，笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚，鸡和兔各有几只？（）

    • A、兔有5只，鸡有3只。
    • B、兔有3只，鸡有5只。
    • C、兔有4只，鸡有4只。
    • D、兔有2只，鸡有6只。

    正确答案:A

  • 第11题：

    单选题
    有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚。求笼中各有几只鸡和兔？（）
    A

    鸡有23只，兔有12只

    B

    鸡有12只，兔有23只

    C

    鸡有20只，兔有15只

    D

    鸡有15只，兔有20只


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    数据结构与算法里，笼子里有若干只鸡和兔。从上面数，有8个头，从下面数，有26只脚，鸡和兔各有几只？（）
    A

    兔有5只，鸡有3只。

    B

    兔有3只，鸡有5只。

    C

    兔有4只，鸡有4只。

    D

    兔有2只，鸡有6只。


    正确答案： A
    解析： 暂无解析

  • 第13题：

    ：4只小鸟飞人4个不同的笼子里去，每只小鸟都有自己的一个笼子(不同的鸟，笼子也不同)，每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有（ ）种不同的飞法。

    A．16

    B．15

    C．12

    D．9


    正确答案：D

    第1只鸟除了自己的笼子不能进，有3种选择；第2只鸟也有3种选择：剩下的2只鸟只有1种选择。故不同的飞法共有3×3=9种。

  • 第14题：

    ：有一列数，第1个数是35，第2个数是25，从第3个数开始，每个数都是它前面两个数的平均数。这列数的第15个数的整数部分是（ ）。

    A．19

    B．24

    C．28

    D．30


    正确答案：C

    第3个数为(35+25)÷2=30，第4个数为(25+30)÷2=27.5，第5个数为(30+27．5)÷2=28.75，第6个数为28.125，此后每个数都小于第5个数，大于第6个数。所以第5个数的整数部分是28。因此，本题正确答案为C。

  • 第15题：

    有若干个各不相同的自然数，它们的平均数是10，如果从这些数中去掉最大的一个，则余下的平均数为9；如果去掉最小的一个，则余下的平均数为11，则这些数最多有多少个?（ ） A．11 B．10 C．9 D．8


    正确答案：A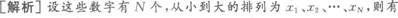



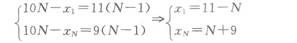
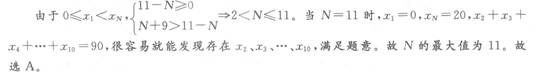
  • 第16题：

    从1、2、…、11这十一个自然数中，随机抽取五个不同的数，则这五个数的和为偶数的取法有多少种?(　)

    A、 220　　B、 226　　C、 231　　D、 236


    B　解析：本题可分三种情况考虑：（1）取5个偶数，共有 ＝1（ 种）取法；（2）取3个偶数，再取2个奇数，共有 ＝150（种）取法；（3）取1个偶数 ，再取4个奇数，共有 ＝75（种）取法。所以总的取法有1＋150＋75＝226（种）。本题正确答案为B

  • 第17题：

    在一个大笼子里关了一些鸡和一些兔子。数它们的头，一共有36个；数它们的腿一共有100条。问鸡和兔各多少只？（ ）

    A.鸡21只，兔13只

    B.鸡23只，兔16只

    C.鸡22只，兔14只

    D.鸡23只，兔15只


    正确答案：C
    C【解析】假设36只全是鸡，就应有72条腿（2×36），这就比题目所说的“100条腿”少了28条腿。为什么“腿”会少呢？很显然，是我们把四条腿的兔子当成了两条腿的鸡。由此即可求出兔子的只数，列式为：（100-2×36）÷（4-2）=28÷2=14（只）；鸡的只数为：36-14=22（只）。

  • 第18题：

    丁丁和宁宁各有一只盒子，里面都放着棋子，两只盒子里的棋子一共是270粒。丁丁从自己的盒子里拿出÷的棋子放入宁宁的盒子里后，宁宁盒子里的棋子数恰好增加亡。原来宁宁有棋子多少粒?（ ）

    A．180

    B．150

    C．120

    D．145


    正确答案：B
    根据题意，可知丁丁原有棋子的1/4恰好等于宁宁原有棋子的1/5。即丁丁原有棋子是宁宁的4/5。270÷(1+4/5)=150(粒)。

  • 第19题：

    从1、3、9、27、81、243这六个数中，每次取出若干个数(每次取数，每个数只能取一次)求和，可以得到一个新数，一共有63个数。如果把它们以小到大依次排列起来是：
    1，3，4，9，10，12，…。那么，第60个数是（　　）。

    A.363
    B.361
    C.360
    D.355

    答案：C
    解析：
    由题目可知，第63个数是364(即6个数之和)，第62个数是364-1=363，第61个数是364-3=361，第60个数是364-1-3=360。

  • 第20题：

    一个盒子里有黑棋子和白棋子若干粒，若取出一粒黑子，则余下的黑子数与白子数之比为9：7，若放回黑子，再取出一粒白子，则余下的黑子数与白子数之比为7：5，那么盒子里原有的黑子数比白子数多：

    A.5枚
    B.6枚
    C.7枚
    D.8枚

    答案：C
    解析：
    棋子总数减1是9+7和7+5的倍数，因此设棋子总数为48n+1，48为16和12的最小公倍数。根据黑子数量得等式27n+1=28n，解得n=1。因此黑子有28枚，白子有21枚，黑子比白子多7枚。

  • 第21题：

    有关“确定表元的数据来源于报表系统自身取数”叙述不正确的有（）

    • A、从软件其他模块取数
    • B、从同一报表的不同表页取数
    • C、从系统中其他报表取数
    • D、从同一表页的不同单元取数

    正确答案:A

  • 第22题：

    钢丝绳从结构组成（股数和丝数）上分有6×19，6×24，9×37等几种。


    正确答案:正确

  • 第23题：

    单选题
    4只小鸟飞入4个不同的笼子里去，每只小鸟都有自己的一个笼子（不同的鸟，笼子也不相同），每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有多少种不同的飞法？（）。
    A

    7

    B

    8

    C

    9

    D

    10


    正确答案： D
    解析： 暂无解析

相关内容