设x是一维数组，x的倒数第3个元素表示为（）设y为二维数组，要删除y的第34行和48列，可使用命令（）
题目
设x是一维数组，x的倒数第3个元素表示为（）设y为二维数组，要删除y的第34行和48列，可使用命令（）
相似考题
更多“设x是一维数组，x的倒数第3个元素表示为（）设y为二维数组，要删除y的第34行和48列，可使用命令（）”相关问题
-
第1题：
给出发下定义: char x[]="abcdefg"; char y[]={'a', 'b', 'c', 'd', 'e', 'f', 'g' };则正确的叙述为______。
A．数组x和数组y等价
B．数组x和数组y的长度相同
C．数组x的长度大于数组y的长度
D．数组x的长度小于数组y的长度
正确答案：C
-
第2题：
设int x[ ]={2，4，6，8}，y，*p=&x[1]；则执行语句y=(*--p)++；后数组元素x[0]的值为 ______。
A．2
B．3
C．4
D．5
正确答案：B
-
第3题：
设二维随机变量(X，Y)的概率密度为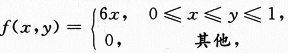
则P{X+Y≤1}=_______.答案：解析：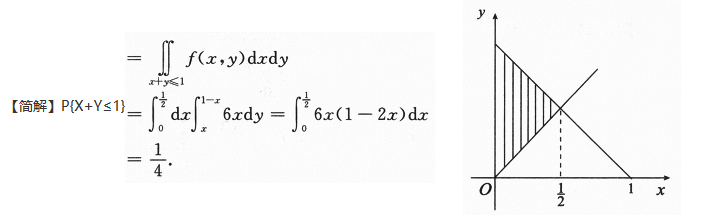
-
第4题：
设二维随机变量(X,Y)的联合密度为f(x,y)=
(1)求c；(2)求X,Y的边缘密度,问X,y是否独立？
(3)求Z=max(X,Y)的密度.答案：解析：
-
第5题：
设随机变量(X，Y)服从二维正态分布，其概率密度为f(x,y)=1/2π
答案：A解析：提示 (X，Y)~N(0，0，1，1，0)，X~N(0，1)，Y~N(0，1)，E(X2+Y2) =E(X2)+E(Y2)，E(X2)=D(X) + (E(X) )2 -
第6题：
设二维随机变量(X，Y)服从二维正态分布，则随机变量ζ=X+Y与η=X-Y不相关的充分必要条件为
答案：B解析：
-
第7题：
若给出以下定义：charx[]=”abcdefg”；chary[]={‘a’，’b’，’c’，’d’，’e’，’f’，’g’}；则正确的叙述为（）。
- A、数组x和数组y等价
- B、数组x和数组y的长度相同
- C、数组x的长度大于数组y的长度
- D、数组y的长度大于数组x的长度
正确答案:C -
第8题：
设浮点数的格式为：阶码 5 位，尾数 6 位，均用补码表示，请计算 X+Y 和 X-Y。（阶码和尾数均用补码计算）。【＊＊，★，包捷 4.8，编号 2.3】 X=15/64，Y=-25/256
正确答案:方法一（双符号法）
X.1111X2-6=0.1111X2-10
[X]浮=11，111000.11110
Y.-11101X2-8=-0.11101X2-11
[Y]浮=11，110111.00011
计算X+Y：
1.对阶
Y.向X对齐，Y的尾数右移1位。
[Y]浮=11，111011.10001（1）
2.尾数相加
[X]尾+[Y]尾=00.11110+11.10001（1）=00.01111（1）
3.结果规格化：双符号00，无溢出。一个前导0，左规一位。
[Z]尾=00.11111
[Z]阶=11，1110-1=11，11014. 舍入：[X+Y]浮=1,1101 0.11111计算 X-Y：5. 对阶Y 向 X 对齐，Y 的尾数右移 1 位。[Y]浮=11,1110 11.10001(1)6. 尾数相减[X]尾-[Y]尾=00.11110-11.10001(1)=00.11110+(100.00000-11.10001(1))=01.01100(1)7. 结果规格化：双符号 01，有溢出。右规一位，阶码+1[X-Y]尾=00.10110(01)[X-Y]阶=11,1110+1=11,11118. 舍入[X-Y]浮=1,1111 0.10110 -
第9题：
设字长为8位，X=10100101，Y=11000011，求X∧Y， X∨Y ，X Y的结果。
正确答案: X∧Y=10000001 ， X∨Y =11100111 ， X Y=01100110 -
第10题：
设随机变量X的概率密度为fX（x），随机变量Y的概率密度为fY（y），则二维随机变量（X、Y）的联合概率密度为fX（x）fY（y）。
正确答案:错误 -
第11题：
填空题设doubley[4][5]；，则数组y中元素的个数是（）。正确答案： 20解析： 暂无解析 -
第12题：
单选题设随机变量（X，Y）服从二维正态分布，且X与Y不相关，fX（x），fY（y）分别表示X，Y的概率密度，则在Y＝y的条件下，X的条件概率密度fX|Y（x|y）为（ ）。AfX（x）
BfY（y）
CfX（x）fY（y）
DfX（x）/fY（y）
正确答案： C解析：
因为（X，Y）服从二维正态分布，且相关系数ρ＝0，故X，Y相互独立，故fX|Y（x|y）＝f（x，y）/fY（y）＝fX（x）fY（y）/fY（y）＝fX（x）。 -
第13题：
设有定义：
int x[2][3]；
则以下关于二维数组X的叙述错误的是
A.元素x[0]可看作是由3个整型元素组成的一维数组
B.数组x可以看作是由X[0]和X[1]两个元素组成的一维数组
C.可以用x[0]=0；的形式为数组所有元素赋初值0
D.x[O]和x[1]是数组名，分别代表一个地址常量
正确答案：C
x[o]可看作是由3个整型元素组成的一维数组，不可以用语句x[0]=0；为数组所有元素赋初值0。因此C选项正确。 -
第14题：
设二维随机变量(X,Y)服从二维正态分布,且X～N(1,3^2),Y～N(0,4^2),且X,Y的相
关系数为－
,又设Z=
(1)求E(Z),D(Z)；(2)求
；(3)X,Z是否相互独立？为什么？答案：解析：【解】(1)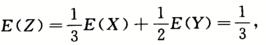
(2)
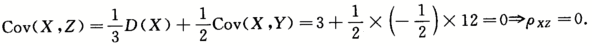
(3)因为(X，Y)服从二维正态分布，所以Z服从正态分布，同时X也服从正态分布，又X，
Z不相关，所以X，Z相互独立. -
第15题：
设二维随机变量(X,Y)的联合密度函数为f(x,y)=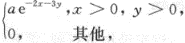
则a=_______,P(X>Y)=_______.答案：解析：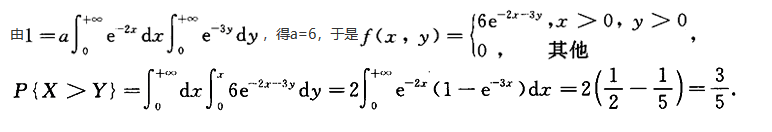
-
第16题：
设二维离散型随机变量(X，Y)的概率分布为
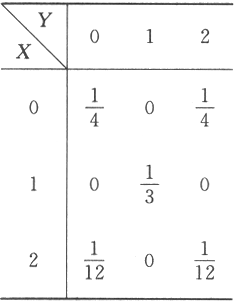
(Ⅰ)求P{X=2Y)；
(Ⅱ)求Cov(X-Y，Y).答案：解析：
-
第17题：
设X和Y分别表示扔n次硬币出现正面和反面的次数,则X,Y的相关系数为().
答案：A解析：设正面出现的概率为p，则X～B（n，p），Y=n-X～B（n，1-p），E(X)=np,D(X)=np(1-p),E(Y)=n(1-p),D(Y)=np(1-p),Cov(X，Y)=Cov(X，n-X)=Cov(X，n)-Cov(X，X)，因为Cov(X,n)=E(nX)-E（n）E(X)=nE(X)-nE(X)=0,Cov(X，X)=D(X)=np（1-p），所以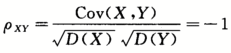
，选(A) -
第18题：
设一维数组中有n个数组元素，则读取第i个数组元素的平均时间复杂度为()。
答案：C解析：数组是随机存取的结构，所以读取第i个节点的时间复杂度为0(1)。 -
第19题：
设浮点数的格式为：阶码 5 位，尾数 6 位，均用补码表示，请计算 X+Y 和 X-Y。（阶码和尾数均用补码计算）。【＊＊，★，包捷 4.8，编号 2.3】 X=-1.625，Y=5.25
正确答案:1）方法一：（双符号法）
X.-1.625=-1.101B=-0.1101*21
[X]浮=00，000111.00110
Y.5.25=101.01B=0.10101*211
[Y]浮=00，001100.10101
计算X+Y：
对阶
[X]阶<[Y]阶，X向Y对齐。X尾数右移2位，X阶码+2
[X]浮=00，001111.11001（10）
尾数相加
[X]尾+[Y]尾=11.11001（10）+00.10101=00.01110（10）（mod4）
结果规格化：双符号00，无溢出。但有一个前导0，需要左规1位：尾数左移1位，阶码-1
[X+Y]尾=00.11101（0）
[X+Y]阶=00，0011-1=00，0011+（100，0000-1）=00，0011+11，1111=00，0010（无溢出）
舍入
[X+Y]浮=0，00100.11101//舍去0
计算X-Y：
对阶
[X]阶<[Y]阶，X向Y对齐。X尾数右移2位，X阶码+2
[X]浮=00，001111.11001（10）
尾数相减
[X]尾-[Y]尾=11.11001（10）+（100.00000-00.10101）=11.11001+11.01011=11.00100（10）
结果规格化：双符号11，无溢出。结果已规格化
舍入：入1
[X-Y]浮=0，00111.00101 -
第20题：
设（X，Y）服从二维正态分布，则cov（X，Y）=0是X与Y相互独立的（）条件。
正确答案:充要 -
第21题：
设doubley[4][5]；，则数组y中元素的个数是（）。
正确答案:20 -
第22题：
填空题设x是一维数组，x的倒数第3个元素表示为（）设y为二维数组，要删除y的第34行和48列，可使用命令（）正确答案： x（end-2）,y（34，：）=[],y（：，48）=[]解析： 暂无解析 -
第23题：
多选题数学期望的性质包括（）A设c为常数，则E（c）＝c
B设X为随机变量，α为常数，则E（αX）＝αE（X）
C设X、y是两个随机变量，则E（X±Y）＝E（X）＋E（Y）
D设X、y是相互独立的随机变量，则E（XY）＝E（X）E（Y）
E设c为常数，则E（c）＝0。
正确答案： A,C解析： 设X、y是相互独立的随机变量，则E（XY）＝E（X）E（Y）。