矩估计法的主要思想是：以（）作为相应的总体矩的估计，以（）作为总体矩的函数的估计。

题目

矩估计法的主要思想是：以（）作为相应的总体矩的估计，以（）作为总体矩的函数的估计。

相似考题

1.由样本估计总体参数的方法很多,我国工程水文计算中常用的参数估计方法有()。A.适线法B.矩法C.权函数法D.概率权重矩法

2.参数估计分为()和区间估计A、矩法估计B、似然估计C、点估计D、总体估计

3.泊松分布的参数λ的矩法估计是（ ）。A.用方差作为λ的矩法估计B.用均值作为λ的矩法估计C.用标准差作为λ的矩法估计D.用极差作为λ的矩法估计

4.用矩估计法对总体方差作点估计时，要用样本的（ ）估计。A．一阶原点矩 B．二阶原点矩C．一阶中心矩 D．二阶中心矩

更多“矩估计法的主要思想是：以（）作为相应的总体矩的估计，以（）作为总体矩的函数的估计。”相关问题

  • 第1题：

    矩法估计的缺点是（ ）。
    A.要求知道总体的分布 B.估计不惟一
    C.不准确 D.总体的分布难以确定


    答案：B
    解析：
    矩法估计简单实用，所获得的估计量通常也有较好的性质，但缺点是有时估计不惟一。

  • 第2题：

    下列关于矩法估计的说法正确的有（ ）。
    A.矩法估计是求点估计的方法
    B.矩法估计简单而实用，所获得的估计量通常(尽管不总是如此)有较好性质
    C.但是应该注意到，矩法估计不一定总是最有效的，而且估计不惟一
    D.矩法估计是用某种方法获得未知参数的点估计的方法
    E.矩法估计是惟一最有效的


    答案：A,B,C,D
    解析：
    获得未知参数的点估计的方法称为矩法估计。这种方法可概括为：①用样本矩去估计相应的总体矩；②用样本矩的函数去估计相应总体矩的函数。矩法估计简单而实用，所获得估计量通常有较好性质。但是矩法估计不一定是最有效的，而且有时估计也不惟一。

  • 第3题：

    设总体X～U(θ,θ),X1,X2,…,Xn是来自总体X的样本,求θ1,θ2的矩估计和最大似然估计.


    答案：
    解析：

  • 第4题：

    设总体X~N(0,σ2)，X1，X2，...Xn是自总体的样本，则σ2的矩估计是:


    答案：D
    解析：
    提示 注意 E(x)=0，σ2=D(x)=E(x2) - [E(x)]2=E(x2)，σ2也是x的二阶原点矩，σ2的矩估计量是样本的二阶原点矩。

  • 第5题：

    统计参数的估计时一般可采用（）来调整初步估计的参数。

    • A、概率权重矩法
    • B、适线法
    • C、参数估计法
    • D、矩法

    正确答案:B

  • 第6题：

    用样本的矩去估计总体的矩，从而获得有关参数的估计量，称之为（）。

    • A、矩估计法
    • B、点估计法
    • C、最小二乘法
    • D、最大似然估计法

    正确答案:A

  • 第7题：

    填空题
    矩估计法的主要思想是：以（）作为相应的总体矩的估计，以（）作为总体矩的函数的估计。

    正确答案： 样本矩,样本矩的函数
    解析： 暂无解析

  • 第8题：

    多选题
    下列关于矩法估计的说法正确的有（　　）。
    A

    矩法估计是求点估计的方法

    B

    矩法估计简单而实用，所获得的估计量通常（尽管不总是如此）有较好性质

    C

    但是应该注意到，矩法估计不一定总是最有效的，而且估计不惟一

    D

    矩法估计是用某种方法获得未知参数的点估计的方法

    E

    矩法估计是惟一最有效的


    正确答案： D,E
    解析：
    获得未知参数的点估计的方法称为矩法估计。这种方法可概括为：①用样本矩去估计相应的总体矩；②用样本矩的函数去估计相应总体矩的函数。矩法估计简单而实用，所获得估计量通常有较好性质。但是矩法估计不一定是最有效的，而且有时估计也不惟一。

  • 第9题：

    单选题
    矩估计的基本原理是（）
    A

    用样本矩估计总体矩

    B

    使得似然函数达到最大

    C

    使得似然函数达到最小

    D

    小概率事件在一次试验中是不可能发生的


    正确答案： C
    解析： 暂无解析

  • 第10题：

    单选题
    用样本的矩去估计总体的矩，从而获得有关参数的估计量，称之为（）。
    A

    矩估计法

    B

    点估计法

    C

    最小二乘法

    D

    最大似然估计法


    正确答案： B
    解析： 暂无解析

  • 第11题：

    单选题
    统计参数的估计时一般可采用（）来调整初步估计的参数。
    A

    概率权重矩法

    B

    适线法

    C

    参数估计法

    D

    矩法


    正确答案： C
    解析： 统计参数的估计可按下列步骤进行：①初步估计参数。一般首先采用参数估计法（如矩法），估计统计参数。②采用适线法来调整初步估计的参数。调整时，可选定目标函数求解统计参数，也可采用经验适线法。③适线调整后的统计参数应根据本站径流、洪峰、不同时段洪量统计参数和设计值的变化规律，以及上下游、干支流和邻近流域各站的成果进行合理性检查，必要时可作适当调整。

  • 第12题：

    单选题
    用样本均值估计总体均值的构造点估计的方法是(    )
    A

    最小二乘法

    B

    贝叶斯估计法

    C

    最大似然估计法

    D

    矩估计法


    正确答案： A
    解析：

  • 第13题：

    参数的矩法估计是指（ ）。
    A.用样本矩估计总体相应的矩
    B.用总体矩估计样本相应的矩
    C.用样本矩的函数估计总数矩相应的函数
    D.用总体矩的函数估计样本相应的矩的函数
    E.用总体矩估计样本相应的矩的函数


    答案：A,C
    解析：
    矩法估计这种方法可概括为：①用样本矩去估计相应的总体矩；②用样本矩的函数去估计相应总体矩的函数。

  • 第14题：

    设总体X的分布函数为
    　　
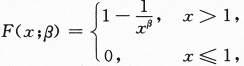
    　　其中未知参数β>1，X1，X2，…，Xn为来自总体X的简单随机样本，求：
    　　(Ⅰ)β的矩估计量；(Ⅱ)β的最大似然估计量.


    答案：
    解析：

  • 第15题：

    点估计是依据样本估计总体分布中所含的未知参数或未知参数的函数，通常它们是总体的某个特征值，如数学期望、方差和相关系数，构造点估计常用的方法有（ ）。

    Ⅰ.矩估计法

    Ⅱ.最大似然估计法

    Ⅲ.最小二乘法

    Ⅳ.顺序统计量法

    A、Ⅰ,Ⅱ
    B、Ⅱ,Ⅲ
    C、Ⅰ,IV
    D、Ⅰ,Ⅱ,Ⅲ,Ⅳ

    答案：A
    解析：
    A
    构造点估计常用的方法有：①矩估计法：用样本矩估计总体矩，如用样本均值估计总体均值；②最大似然估计法：利用样本分布密度构造似然函数来求出参数的最大似然估计；

  • 第16题：

    设总体X服从均匀分布U（1，θ），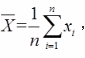

    则θ的矩估计为（　　）。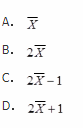


    答案：C
    解析：
    均匀分布U（a，b）的概率密度为：

  • 第17题：

    矩估计的基本原理是（）

    • A、用样本矩估计总体矩
    • B、使得似然函数达到最大
    • C、使得似然函数达到最小
    • D、小概率事件在一次试验中是不可能发生的

    正确答案:A

  • 第18题：

    矩法就是用样本矩估计总体矩，并通过矩与参数之间的关系，来估计频率曲线的参数的方法。


    正确答案:正确

  • 第19题：

    多选题
    由样本估计总体参数的方法很多，我国工程水文计算中常用的参数估计方法有（）。
    A

    适线法

    B

    矩法

    C

    权函数法

    D

    概率权重矩法


    正确答案： B,C
    解析： 暂无解析

  • 第20题：

    单选题
    矩法估计的缺点是（　　）。
    A

    要求知道总体的分布

    B

    估计不惟一

    C

    不准确

    D

    总体的分布难以确定


    正确答案： D
    解析：
    矩法估计简单实用，所获得的估计量通常也有较好的性质，但缺点是有时估计不惟一。

  • 第21题：

    多选题
    参数的矩法估计是指（　　）。
    A

    用样本矩估计总体相应的矩

    B

    用总体矩估计样本相应的矩

    C

    用样本矩的函数估计总数矩相应的函数

    D

    用总体矩的函数估计样本相应的矩的函数

    E

    用总体矩估计样本相应的矩的函数


    正确答案： A,D
    解析：
    矩法估计这种方法可概括为：①用样本矩去估计相应的总体矩；②用样本矩的函数去估计相应总体矩的函数。

  • 第22题：

    单选题
    两点分布b(1，P)的参数P的估计是(　　)。
    A

    用方差做为P的矩法估计

    B

    用均值做为P的矩法估计，用频率去估计概率

    C

    用标准差做为P的矩法估计

    D

    用极差做为P的矩法估计


    正确答案： B
    解析： 暂无解析

  • 第23题：

    判断题
    矩法就是用样本矩估计总体矩，并通过矩与参数之间的关系，来估计频率曲线的参数的方法
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

相关内容