在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。
题目
在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。
相似考题
更多“在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。”相关问题
-
第1题：
设X~N(μ，0.09)从中随机抽取样本量为4的样本，其样本均值为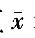
，则总体均值μ的0.95的置信区间为（）。
A.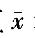
±0.15u0.95 B.
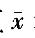±0.15u0.975 C. 
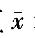±0.3u0.95 D.
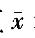±0.3u0.975答案：B解析：
-
第2题：
下列表述中正确的有( )。A.总体均值的置信区间都是由样本均值加减估计误差得到
B.在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
C.当样本量n充分大时，样本均值的分布近似服从正态分布
D.当总体服从正态分布时，无论样本量大小，样本均值一定服从正态分布
E.对总体均值进行区间估计时，不需要考虑总体方差是否已知答案：A,B,D解析：选项C错误，若总体为未知的非正态总体，当样本量n充分大时，样本均值的分布近似服从正态分布；选项E错误，对总体均值进行区间估计时，需要考虑总体方差是否已知，当总体方差未知时，需要用样本方差来代替总体方差。 -
第3题：
从一个服从正态分布的总体中随机抽取样本容量为n的样本，在95％的置信度下对总体均值进行估计的结果为20±0.08。如果其他条件不变，样本容量扩大到原来的4倍，则总体均值的置信区间应该是( )。
A.20±0.16
B.20±0.04
C.80±0.16
D.80±0.04答案：B解析：
-
第4题：
从一个服从正态分布的总体中随机抽取样本容量为 n 的样本，在 95％的置信度下对总体均值进行估计的结果为 20±0.08。如果其他条件不变，样本容量扩大到原来的 4 倍，总体均值的置信区间应该是( )。
A.20±0.16
B.20±0.04
C.80±0.16
D.80±0.04答案：B解析：在正态分布下，总体均值区间估计为
故样本容量扩大到原来的 4 倍，误差项变为原来的一半。 -
第5题：
已知总体分布为正态，方差为100。从这个总体中随机抽取样本容量为16的样本，样本平均数为60，那么总体均值 的99%的置信区间为A.[50.10,69.90]
B.[53.55,66.45]
C.[56.08,63.92]
D.[55.10,64.90]答案：B解析：本题考查的是总体平均数的估计方法。当总体方差已知时，若总体分布为正态，或者总体分布为非正态，但样本容量超过30，置信区间的公式是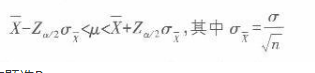
将本题中各项数据代入，则求得置信区间为[ 53.55，66.45]。 -
第6题：
在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是（）。
- A、样本容量太小
- B、估计量缺乏有效性
- C、选择的估计量有偏
- D、抽取样本时破坏了随机性
正确答案:A -
第7题：
下列表述中，错误的是（）。
- A、总体均值的置信区间都是由样本均值加减估计误差得到
- B、在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
- C、当样本量n充分大时，样本均值的分布近似服从正态分布
- D、当总体服从正态分布时，样本均值不服从正态分布
- E、A总体均值进行区间估计时，不需要考虑总体方差是否已知
正确答案:D,E -
第8题：
在估计某一总体均值时，随机抽取n个单位作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是（）
- A、样本容量太小
- B、估计量缺乏有效性
- C、选择的估计量有偏
- D、抽取样本时破坏了随机性
正确答案:A -
第9题：
从均值为200、标准差为50的总体中，抽取n=100的简单随机样本，用样本均值x估计总体均值，x的数学期望是（）
正确答案:200 -
第10题：
填空题从均值为200、标准差为50的总体中，抽取n=100的简单随机样本，用样本均值x估计总体均值，x的数学期望是（）正确答案： 200解析： 暂无解析 -
第11题：
判断题在估计某一总体均值时，随机抽取n个单元作样本，用样本均值作估计量，在构造置信区间时，发现置信区间太宽，其主要原因是样本容量太小。A对
B错
正确答案： 对解析： 暂无解析 -
第12题：
填空题从均值为200、标准差为50的总体中，抽取n=100的简单随机样本，用样本均值x估计总体均值，标准差是（）正确答案： 5解析： 暂无解析 -
第13题：
下列表述中，错误的是（）。A.总体均值的置信区间都是由样本均值加减估计误差得到
B.在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
C.当样本量n充分大时，样本均值的分布近似服从正态分布
D.当总体服从正态分布时，样本均值不服从正态分布
E.对总体均值进行区间估计时，不需要考虑总体方差是否已知答案：D,E解析：当总体服从正态分布时，样本均值也服从正态分布。对总体均值进行区间估计时，需要分两种情况：方差已知和方差未知。 -
第14题：
已知总体服从正态分布，且总体标准差σ，从总体中抽取样本容量为n的产品，测得其样本均值为x，在置信水平为1-a=95％下，总体均值的置信区间为（ ）
答案：A解析： -
第15题：
一个随机抽取的样本，样本均值，在95%的置信度下总体均值置信区间为。下面说法正确的是（）。A．总体中有95%的数据在12到18之间
B．样本中有95%的数据在12到18之间
C．假如有100个样本被抽取，则会有95个样本均值在12到18之间
D．样本中的数据落在12到18之间的概率为95%答案：D解析： -
第16题：
随机抽取一个样本容量为100的样本，其均值?X-80，标准差s=10，所属总体均值 的95%的置信区间是A.[78．04,81．96]
B.[60．40,99．60]
C.[76．08,83．92]
D.[79．80,80．20]答案：A解析：本题总体方差未知，使用样本方差作为总体方差的估计值(100)，利用标准误的公式求标准误为1（方差除以样本容量的平方根）。本题应查t表求95%的置信区间的t值，因为样本容量较大(100)，可以z值进行估计，Z0．05／2为1．96。因此总体均值的95%的置信区间应该为[80 -1．96×1，80 +1．96×1]，即[78．04,81．96]。 -
第17题：
下列关于区间预测说法正确的有（ ）。
Ⅰ.样本容量n越大，预测精度越高
Ⅱ.样本容量n越小，预测精度越高
Ⅲ.置信区间的宽度在x均值处最小
Ⅳ.预测点xo离x均值越大精度越高
A、Ⅰ.Ⅱ.Ⅲ
B、Ⅰ.Ⅱ.Ⅳ
C、Ⅰ.Ⅲ
D、Ⅰ.Ⅲ.Ⅳ答案：C解析：在预测时要注意预测点Xo与估计模型时用的样本x1, x2,…,xo的距离，如果xo与所估计模型的样本偏离太大，预测效果会很差。一般地:①样本容量n越大，预测精度越高，反之预测精度越低;②样本容量一定时，置信区间的宽度在X均值处最小，预测点xo离x均值越小精度越高，越远精度越低。 -
第18题：
下列样本说法中正确的有（）。
- A、样本均值是总体均值的无偏估计量
- B、样本比例是总体比例的无偏估计量
- C、样本均值是总体均值的一致估计量
- D、样本标准差是总体标准差的无偏估计量
- E、样本方差是总体方差的无偏估计量
正确答案:A,B,C,E -
第19题：
从均值为200、标准差为50的总体中，抽取n=100的简单随机样本，用样本均值x估计总体均值，标准差是（）
正确答案:5 -
第20题：
已知正态总体标准差为10，样本量n=25，置信水平为95%，Z=1.96，样本均值=105.36。则以下正确的有（）
- A、样本均值的标准差为10
- B、样本均值的标准差为2
- C、样本均值的置信区间为（101.44，109.28）
- D、总体均值的置信区间为（101.44，109.28）
正确答案:B,D -
第21题：
单选题一个随机抽取的样本，样本均值x(＿)＝15，在95%的置信度下总体均值置信区间为15±3。下面说法正确的是（ ）。[2015年中级真题]A总体中有95%的数据在12到18之间
B样本中有95%的数据在12到18之间
C假如有100个样本被抽取，则会有95个样本均值在12到18之间
D样本中的数据落在12到18之间的概率为95%
正确答案： B解析：
95%的置信度表示在多次抽样中有95%的样本得到的区间包含总体均值。它的真正意义是如果做了100次抽样，大概有95次找到的区间包含总体均值，有5次找到的区间不包含总体均值。 -
第22题：
单选题对于给定的总体和抽样方式以及样本容量，样本指标取值的概率分布就称为A抽样估计
B抽样分布
C样本均值
D置信区间
正确答案： D解析： 暂无解析 -
第23题：
多选题下列表述中，错误的是（ ）。[2011年初级真题]A总体均值的置信区间都是由样本均值加减估计误差得到
B在小样本情况下，对总体均值的估计都是建立在总体服从正态分布的假定条件下
C当样本量n充分大时，样本均值的分布近似服从正态分布
D当总体服从正态分布时，样本均值不服从正态分布
E对总体均值进行区间估计时，不需要考虑总体方差是否已知
正确答案： B,A解析：
当总体服从正态分布时，样本均值也服从正态分布。对总体均值进行区间估计时，需要分两种情况：方差已知和方差未知。