有四个自然数A、B、C、D，它们的和不超过400，并且A除以B商是5余5，A除以C商是6余6，A除以D商是7余7。那么，这四个自然数的和是（）。A、216B、108C、314D、348

题目

有四个自然数A、B、C、D，它们的和不超过400，并且A除以B商是5余5，A除以C商是6余6，A除以D商是7余7。那么，这四个自然数的和是（）。

  • A、216
  • B、108
  • C、314
  • D、348
相似考题

1.某不超过200的自然数除以5余1，除以7余2，除以11余2，问这个数除以13余数是多少?A．0B．3C．5D．7

2.三位数的自然数N满足：除以6余3，除以5余3，除以4也余3，则符合条件的自然数N有几个？（）A.8 B.9 C.15 D.16

3.有一个自然数“x”，除以4的余数是3，除以5的余数是4，问“x”除以20的余数是多少?（ ）

4.有一个自然数z， 除以3的余数是2， 除以4的余数是3， 问z除以12的余数是( )。A．1B．5C．9D．11

更多“有四个自然数A、B、C、D，它们的和不超过400，并且A除以B商”相关问题

  • 第1题：

    有四个自然数A、B、C、D，它们的和不超过400，并且A除以8商是5余5，A除以C商是6余6，A除以D商是7余7。那么，这四个自然数的和是（ ）。

    A．216

    B．108

    C．314

    D．348


    正确答案：C
    根据题意可知A是5、6、7的公倍数，又因为5、6、7的最小公倍数为210，则A应该为210，否则如果A等于420，630，…则A、B、C、D的和显然要大于400。A等于210，则B等于41，C等于34，D等于29，则四个数的和显然为314，故选C。

  • 第2题：

    (7分)自然x是一个三位数，已知X除以8的商是a、余数是b,x除以9的商是c、余数是d，且a+d=13，求所有满足条件的自然数x。


    答案：
    解析：
    由于a，b，c，d均为自然数，且a+d=13，所以a∈]0，13]。又有x是一个三位数，x除以8的商是0，故a=12或13。 若a=12，x是一个三位数，且b∈[0，7]，故满足条件x可以为100，101，102，103，此时d=1，要满足x除以9余数为1．100成立；
    若a=13，x是一个三位数，且b∈[0，7]，故满足条件x可以为104，105，106，107，108，109，110，111，此时d=0，要满足x除以9余数为0，只有108。
    综上，满足条件的自然数x有100，108。

  • 第3题：

    有一个自然数“X”，除以3的余数是2，除以4的余数是3，问“X”除以12的余数是多 少？（ ）
    A. 1 B. 5 C. 9 D. 11


    答案：D
    解析：
    本题用代入法求解最为简单，任意找一个符合“除以3的余数是2，除以4 的余数是3”的数，如11，则除以12的余数就是11。故本题选D。

  • 第4题：

    单选题
    有两个自然数，它们的和等于297，它们的最大公约数与最小公倍数之和等于693。这两个自然数的差等于多少？（　　）
    A

    33

    B

    27

    C

    11

    D

    9


    正确答案： C
    解析：
    设这两个数是AM、BM，M是这两个数的最大公约数，其中A、B、M均为整数。AM＋BM＝（A＋B）×M＝297，M＋A×B×M＝（1＋A×B）×M＝693，所以M是297和693的公约数。297和693的最大公约数为99。99＝32×11，把M＝1，3，9，11，33，99分别代入两个式子试算。①（A＋B）×1＝297，（1＋A×B）×1＝693，无解；②（A＋B）×3＝297，（1＋A×B）×3＝693，无解；③（A＋B）×9＝297，（1＋A×B）×9＝693，无解；④（A＋B）×11＝297，（1＋A×B）×11＝693，无解；⑤（A＋B）×33＝297，（1＋A×B）×33＝693，此时A、B一个是4，一个是5；⑥（A＋B）×99＝297，（1＋A×B）×99＝693，无解。所以⑤符合题意，当M＝33时，一个数是4×33＝132，一个数是5×33＝165，即这两个自然数的差为165－132＝33。

  • 第5题：

    单选题
    有一个自然数“X”，除以3的余数是2，除以4的余数是3，问“X”除以12的余数是多少？（　　）
    A

    1

    B

    5

    C

    9

    D

    11


    正确答案： A
    解析：
    由题目“有一个自然数“X”，除以3的余数为2，除以4的余数为3”可知，X再加上1既可以将3整除，也可以将4整除；3，4的最小公倍数为12，则有X＝12n－1，故X除以12的余数为－1＋12＝11。

  • 第6题：

    有一个自然数“x”，除以3的余数是2，除以4的余数是3，问“x”除以12的余数是多少?( )

    A．1

    B．5

    C．9

    D．11


    正确答案：D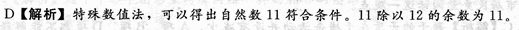

  • 第7题：

    四个连续的自然数的积为1680，它们的和为（ ）。
    A. 26 B. 52 C. 20 D. 28


    答案：A
    解析：
    可用排除法进行判断，答案为26,四个连续自然数为5，6，7，8，应选A。

  • 第8题：

    四个连续自然数的积为1680，它们的和为：

    A. 22
    B. 52
    C. 20
    D. 26

    答案：D
    解析：
    代入法，故答案为D。

  • 第9题：

    单选题
    有四个自然数A，B，C，D，它们的和不超过400，并且A除以B商是5余5，A除以C商是6余6，A除以D商是7余7。那么，这四个自然数的和是（　　）。
    A

    216

    B

    108

    C

    314

    D

    348


    正确答案： C
    解析：
    A＝B×5＋5＝5×（B＋1），A＝C×6＋6＝6×（C＋1），A＝D×7＋7＝7×（D＋1），故A是5、6、7的倍数，又因为5，6，7的最小公倍数是210，所以A是210的倍数，而A不超过400，故A＝210，代入上述余数基本恒等式，得B＝41，C＝34，D＝29，即这四个自然数的和是A＋B＋C＋D＝314。

  • 第10题：

    单选题
    三位数自然数P满足，除以7余2，除以6余2，除以5余2，符合条件的自然数P有多少个？（　　）
    A

    2

    B

    3

    C

    4

    D

    5


    正确答案： D
    解析：
    由“除以7余2，除以6余2，除以5余2”可知，该数减2是7，6，5的公倍数，即2＋210n（n为正整数），且100＜212＋210n＜999，仅当n＝1，2，3，4时符合条件，即P分别为212，422，632，842。

相关内容