设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，9}，则A和B的并集中包含有（）个元素。A、10B、8C、7D、6

题目

设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，9}，则A和B的并集中包含有（）个元素。

  • A、10
  • B、8
  • C、7
  • D、6
相似考题

1.如果要判断一个集合是否是另一个集合的子集,可以使用集合中的方法。()A、ischildsetB、issubsetC、issupersetD、isparentset

2.下面命题为真的是( )。Ⅰ．设A={A1，A2，…，An}是集合A的划分，若Ai∩B≠φ(1≤i≤n)，则{A1∩B，A2∩B，…，An∩A)是集合A的划分Ⅱ．对任意的非空集合A，P(A)-{φ}也可构成A的一个划分A．只有ⅠB．只有ⅡC．都为真D．都不为真

3.设I为整数集合，S={x|x2＜30，x∈I}，T={x|x是素数，x＜20}，R={1，3，5}。(S∩ T)∪R=A．{1，2，3， 5}B．фC．{0}D．{1，3，5，7， 11， 13， 17， 19}

4.设一个集合A={3,4,5,6,7},集合B={1,3,5,7,9},则A减B的差集中包含有()个元素。A.10B.5C.3D.2

更多“设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，”相关问题

  • 第1题：

    下面命题为真的是

    Ⅰ．设A={A1，A2，…，An}是集合A的划分，若Ai∩B≠ф(1≤i≤n)，则{{A1∩B，A2∩B，…，An∩B}}是集合A的划分。

    Ⅱ．对任意的非空集合A，P(A)-{ф}也可构成A的一个划分。

    A．只有Ⅰ

    B．只有Ⅱ

    C．都为真

    D．都不为真


    正确答案：A

  • 第2题：

    只含有一个元素的集合称为单元素集合。()


    参考答案：正确

  • 第3题：

    设∪表示集合的并运算，∩表示集合的交运算，表示集合A的绝对补， A-B表示集合A与B的差，则A-B=(55)。

    A．A∪(A∩B)

    B．A∪

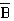
    C．A∩(A∪B)

    D．A∩


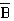    正确答案：D
    解析：设任意两个集合A和B，所有属于A而不属于B的一切元素组成的集合S，称做B对于A的差集(或相对补)，记作S=A-B。设E为全集，对任一集合A关于E的补E-A，称为A的绝对补。根据这个定义，显然A-B=A∩。

  • 第4题：

    设集合A＝{{a}}，B＝{{a}，Φ}，则A∩B＝(51)。

    A．{{a)}

    B．{a}

    C．Φ

    D．{{a}，Φ}


    正确答案：A
    解析：本题考查集合上的基本的运算规则。∩是集合中的交运算，表示是两个集合的公共部分。

  • 第5题：

    设全集U=R，集合A={x｜一5

    答案：
    解析：
    解：全集U=R，A={x｜一5

  • 第6题：

    设全集U=R，集合A={x|-3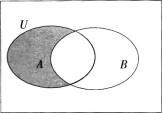


    答案：
    解析：
    {x∣-1≤x<0}。解析：A∩B={x∣-3＜x＜-1}，则阴影部分表示的集合为{x∣-1≤x＜0}。

  • 第7题：

    设R是非空集合，R和R的笛卡尔积到R的一个映射就是运算。


    正确答案:正确

  • 第8题：

    设A为任意有限集合，则包含空集和A在内的全部子集族称作集合A的（），记为（）。


    正确答案:幂集；ρ（A）

  • 第9题：

    设～是集合S的一个等价关系，则所有的等价类的集合是S的一个什么？（）

    • A、笛卡尔积
    • B、元素
    • C、子集
    • D、划分

    正确答案:D

  • 第10题：

    单选题
    设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，9}，则A和B的并集中包含有（）个元素。
    A

    10

    B

    8

    C

    7

    D

    6


    正确答案： C
    解析： 暂无解析

  • 第11题：

    单选题
    宏是指一个或多个（）
    A

    命令集合

    B

    操作集合

    C

    对象集合

    D

    条件表达式集合


    正确答案： C
    解析： 暂无解析

  • 第12题：

    填空题
    设集合A的元素个数为n，则集合A的含奇数个元素的子集的个数是____．

    正确答案： 2n-1
    解析：
    集合A的元素个数为n，则集合A子集的个数是2n，由于含奇数个元素的子集个数和含偶数个子集的个数相等，所以集合A的含奇数个元素的子集的个数是2n－1．

  • 第13题：

    设Y表示集合的并运算，I表示集合的交运算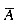，表示集合A的绝对补，A-B月表示集合A与B的差，则A-B=______。

    A．AY(AIB)

    B．AY

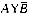
    C．AI(AYB)

    D．AI


    正确答案：D
    解析：设任意2个集合A和B，所有属于A而不属于B的一切元素组成的集合S，称作B对于A的差集(或相对补)，记作S=A-B。设E为全集，对任一集合A关于E的补E-　A，称为A的绝对补。根据这个定义，显然A-B=A∩。

  • 第14题：

    请给出集合A到集合B的映射f的定义.设R是实数集合,f:(0,1)R,证明f是双射。


    答案：A→B的定义是:设A.B是两个集合，如果按照某种对应法则f，对于集合A中的任何一个元素，在集合B中都有唯一的元素和它对应，那么这样的对应(包括集合A.B以及A到B的对应法则f) 叫做集合A到集合B的映射，记作f∶A→B。
    解析：设A,B是两个非空的集合，如果按某一个确定的对应关系f，使对于集合A中的任意一个元素a，在集合B中都有唯一的元素b与之对应，那么就称对应f：A→B为从集合A到集合B的一个映射。


  • 第15题：

    设∪表示集合的并运算，∩表示集合的交运算，A表示集合A的绝对补，A-B表示集合A与B的差，则A-B=______ 。

    A．A∪(A∩B)

    B．A∪B

    C．A∩(A∪B)

    D．A∩B


    正确答案：D
    解析：由集合定义及运算性质可知D正确。

  • 第16题：

    设集合M=｛-2，0，2｝，N=｛0｝，则（　　）


    答案：C
    解析：

  • 第17题：

    [04013设集合M={a，b，c，d}，N=（a，b，c），则集合M∪N=（　　）

    A.{a，b，c}
    B.{d）
    C.{a，b，C，d）
    D.空集

    答案：C
    解析：

  • 第18题：

    设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，9}，则A和B的并集中包括有（）个元素，A和B的交集中包含有（）个元素，A和B的差集中包含有（）个元素。


    正确答案:7；3；2

  • 第19题：

    子集N的对称集合S（N），不是一个普通的集合，而是一个具有（）的集合。

    • A、玄数结构
    • B、常数结构
    • C、有理数结构
    • D、代数结构

    正确答案:D

  • 第20题：

    宏是指一个或多个（）

    • A、命令集合
    • B、操作集合
    • C、对象集合
    • D、条件表达式集合

    正确答案:B

  • 第21题：

    单选题
    设～是集合S的一个等价关系，则所有的等价类的集合是S的一个什么？（）
    A

    笛卡尔积

    B

    元素

    C

    子集

    D

    划分


    正确答案： C
    解析： 暂无解析

  • 第22题：

    填空题
    设A为任意有限集合，则包含空集和A在内的全部子集族称作集合A的（），记为（）。

    正确答案： 幂集,ρ（A）
    解析： 暂无解析

  • 第23题：

    填空题
    设一个集合A={3，4，5，6，7}，集合B={1，3，5，7，9}，则A和B的并集中包括有（）个元素，A和B的交集中包含有（）个元素，A和B的差集中包含有（）个元素。

    正确答案： 7,3,2
    解析： 暂无解析

相关内容