“1、2、3、4、5”这是什么数列？（）A、递增数列B、递减数列C、摆动数列D、无规律的数列

题目

“1、2、3、4、5”这是什么数列？（）

  • A、递增数列
  • B、递减数列
  • C、摆动数列
  • D、无规律的数列
相似考题

1.第 15 题 在数列1/1，2/1，1/2，3/1，2/2，1/3，4/1，3/2，2/3，1/4，5/1……中，9/19居于第（　　）项。A．270B．370C．470D．570

2.设一数列的顺序为1,2,3,4,5,6,通过栈操作,可以得到顺序为3,2,5,6,4,1的输出序列。( )此题为判断题(对，错)。

3.设有一个空栈，栈顶指针为1000H(十六进制，下同)，现有输入序列为1，2，3，4，5，经过PUSH， PUSH，POP，PUSH，POP，PUSH，PUSH后，输出序列是(27)，栈顶指针是(28)。设一数列的顺序为1，2，3，4，5，6，通过栈结构可以排成的顺序数列为(29)，(30)，(31)。A．5，4，3，2，1B．2，1C．2，3D．3，4

4.数列6、-2、5、0、1、4、-1的中位数是A、2B、0.5C、3D、1E、1.9

参考答案和解析
正确答案:A
更多““1、2、3、4、5”这是什么数列？（）”相关问题

  • 第1题：

    在数列1/1，2/1，l/2，3/l，2/2，l/3，4/l，3/2，2/3，1/4，5/l……中，9/19居于第( )项。

    A．270 B．370 C．470 D．570


    正确答案：B

  • 第2题：

    数列：981，（5），（4），109；896，（ ），（4），128

    A.2
    B.3
    C.4
    D.5

    答案：B
    解析：
    第一步，项数较多，考虑多重数列。
    第二步，数列有八项，且每四项有“；”隔开，优先考虑四四分组，分组情况为[981，（5），（4），109]，[896，（所求项），（4），128]，观察发现981＝（5＋4）×109，规律为第一项＝（第二项＋第三项）×第四项，则896＝（所求项＋4）×128，所求项为3。
    因此，选择B选项。

  • 第3题：

    数列：3，2；5，1；6，4；10，2；12，8；

    A.14，1
    B.16，2
    C.18，3
    D.20，4

    答案：D
    解析：
    解析方法一:观察数列特征，分号分成一组。每组两数倍数关系明显，考虑做商数列。前项+后项,得到新数列: 1.5; 5; 1.5; 5; 1.5; ?，此数列为周期数列，? =5。选项D的前项十后项=20+4=5,满足题意。
    方法二:观察数列特征，分号分成-组。每两组之间关系为，前一组两个数的加和=后一组第一个数:前一组两个数差值=后一组第二个数。故所求数为12 +8=20, 12-8=4.

  • 第4题：

    已知首项为1的无穷递缩等比数列的所有项之和为5,q为公比,则q=（ ）

    A.2/3
    B.-2/3
    C.4/5
    D.-4/5
    E.1/2

    答案：C
    解析：

  • 第5题：

    “8、7、6、5、4、3”。这不属于什么数列？（）

    • A、摆动数列
    • B、递减数列
    • C、正项数列
    • D、有穷数列

    正确答案:B

  • 第6题：

    “0，1，1，2，3，5，8，13，21”这个著名数列名为？（）

    • A、大衍数列
    • B、斐波那契数列
    • C、陈景润数列
    • D、卢卡斯数列

    正确答案:B

  • 第7题：

    在直线趋势法中，X是代表时间序列的时间，对时间的编号的方法可以是（）。

    • A、从0开始顺序编写
    • B、从1开始顺序编写
    • C、以公元年号编写
    • D、当数列为奇数项时，编写成-n，-（n-1），-（n-2），…-2，-1，0，1，2，…n-1，n
    • E、当数列为偶数项时，如10项编写成-5，-4，-3，-2，-1，1，2，3，4，5

    正确答案:A,B,C,D

  • 第8题：

    下面（）组数列是斐波那契数列。

    • A、1，1，2，3，5，8，13，21，34，55，„„
    • B、1，2，3，4，5，6，7，8，9，10，11，„„
    • C、1，2，4，8，10，20，40，80，160，320„

    正确答案:A

  • 第9题：

    数列{an}满足an+1=an+2-an，a1=2，a2=5，则a5为（）。

    • A、-3
    • B、-11
    • C、19
    • D、-5

    正确答案:C

  • 第10题：

    单选题
    已知某商业集团2008-2009年各季度销售资料，如表5-1所示。表5-1[img:LzIwMTQtMDgvd21sNzE2LzIwMTQwODI2MTgzNTExMTc1MzkuanBn]则表5-1中，属于时期数列的有()。
    A

    1、2、3

    B

    1、3、4

    C

    2、4

    D

    1、3


    正确答案： A
    解析： 1、3的每个数值反映的是现象在一段时期内发展过程的绝对数之和，故属于时期指标数列;2的每个数值反映的是现象在某一时间上所达到的绝对水平，故属于时点指标数列;4是把同一相对指标在不同时间上的数值按时间先后顺序排列而形成的数列，故属于相对指标数列。

  • 第11题：

    单选题
    下面（）组数列是斐波那契数列。
    A

    1，1，2，3，5，8，13，21，34，55，„„

    B

    1，2，3，4，5，6，7，8，9，10，11，„„

    C

    1，2，4，8，10，20，40，80，160，320„


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    “8、7、6、5、4、3”。这不属于什么数列？（）
    A

    摆动数列

    B

    递减数列

    C

    正项数列

    D

    有穷数列


    正确答案： D
    解析： 暂无解析

  • 第13题：

    已知某商业集团2008-2009年各季度销售资料，如表5-1所示。

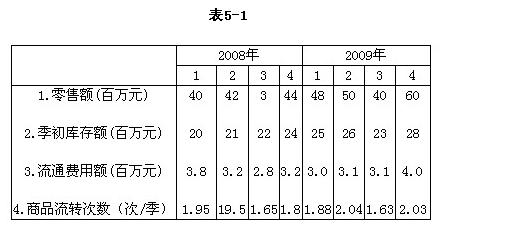
    则表5-1中，属于时期数列的有( )。

    A．1、2、3

    B．1、3、4

    C．2、4

    D．1、3


    正确答案：D
    解析：1、3的每个数值反映的是现象在一段时期内发展过程的绝对数之和，故属于时期指标数列；2的每个数值反映的是现象在某一时间上所达到的绝对水平，故属于时点指标数列；4是把同一相对指标在不同时间上的数值按时间先后顺序排列而形成的数列，故属于相对指标数列。

  • 第14题：

    数列（1/4 +9），（1/2 +9/2 ），（ 3/4 +3），（1+ 9/4），（5/4 + 9/5），……中，数值最小的项是：

    A. 第4项
    B. 第6项
    C. 第9项
    D. 不存在

    答案：B
    解析：

  • 第15题：

    斐波纳奇数列的排列是()。

    A:1，3，5，7，…
    B:2，4，6，8，…
    C:2,3,5,8,…
    D:1,2,3,6,…

    答案：C
    解析：
    斐波纳奇数列的特征之一就是数列中任一数字都等于前两个数字之和。

  • 第16题：

    设an=n2-9n-100(n=1，2，3…)，则数列{an}中取值最小的项为( )。

    A、第4项
    B、第5项
    C、第6项
    D、第4和第5项

    答案：D
    解析：
    将数列％看做一个一元二次多项式，开口向上在对称轴n=4．5处取得最小值。但是数列中n为正整数，故在其附近找最小值。当n=4时，an=-120；当n=5时，an=-120。故取最小值的项为第4项和第5项。故选D。

  • 第17题：

    varmyArr=[1，2，3，4，5]；myArr.shift（）；执行上述代码之后，数组myArr的值是什么（）。

    • A、[1，2，3，4，5]
    • B、[2，3，4，5]
    • C、[]
    • D、[1，2，3，4]

    正确答案:B

  • 第18题：

    一行数列为3、5、2、1、9、7，则中位数为：（）。

    • A、1
    • B、2
    • C、4
    • D、5

    正确答案:C

  • 第19题：

    费波纳奇数列正确的排列是（）

    • A、1，3，5，7...
    • B、2，4，6，8...
    • C、2，3，5，8...
    • D、1，2，3，6...

    正确答案:C

  • 第20题：

    下面数列体现斐波那契特点的是（）

    • A、1、1、2、3、5、8、13、21、……
    • B、2、3、5、8、13、21、……
    • C、2、4、6、8、10、……
    • D、1、1、2、4、6、8、……

    正确答案:A

  • 第21题：

    单选题
    “1、2、3、4、5”这是什么数列？（）
    A

    递增数列

    B

    递减数列

    C

    摆动数列

    D

    无规律的数列


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    数列{an}满足an+1=an+2-an，a1=2，a2=5，则a5为（）。
    A

    -3

    B

    -11

    C

    19

    D

    -5


    正确答案： A
    解析： 暂无解析

  • 第23题：

    单选题
    数列6、-2、5、0、1、4、-l的中位数是（　　）。
    A

    2

    B

    0.5

    C

    3

    D

    1

    E

    1.9


    正确答案： C
    解析： 本题考点是中位数计算。中位数是将原始观察值从小到大排序后，位次居中的那个数。观察值排好序后，当样本量为奇数时，中位数等于位次数居中的数，本例中，-2、-l、0、1、4、5、6，位置居中的数为l，即为中位数；当样本量为偶数时，中位数等于位次居中的两个数的平均数，如-2、-l、1、4、5、6，则中位数等于（1+4）/2=2.5。

相关内容