设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。A、mR2B、mR2/2C、mRω

题目

设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。

  • A、mR2
  • B、mR2/2
  • C、mRω
相似考题

1.有一半径为R的匀质水平圆转台,绕通过其中心且垂直圆台的轴转动,转动惯量为J,开始时有一质量为m的人站在转台中心,转台以匀角速度w0转动,随后人沿着半径向外跑去,当人到达转台边缘时,转台的角速度为()A、w0B、Jw0/mR^2C、Jw0/(J+mR^2)D、Jw0/(J+2mR^2)

2.均质圆盘质量为m，半径为R，再铅垂面内绕o轴转动，图示瞬吋角速度为w，则其对o轴的动量矩和动能的大小为：

3.确定物体绕某个轴的转动惯量，可以由理论计算也可通过实验测定。 (1)用积分计算质量为m，半径为R的均质薄圆盘绕其中心轴的转动惯量。 (2)该圆盘质量未知，可用如图9所示的实验方法测得该圆盘绕中心轴的转动惯量。在圆盘的边缘绕有质量不计的细绳，绳的下端挂一质量为m的重物，圆盘与转轴间的摩擦忽略不计。测得重物下落的加速度为a，求圆盘绕其中心轴的转动惯量。

4.忽略质量的细杆OC=l,其端部固结匀质圆盘圆心，盘质量为m,半径为r。系统以角速度w绕轴O转动。系统的动能是：

更多“设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。A、mR2B、mR2/2C、mRω”相关问题

  • 第1题：

    图示均质圆轮，质量为m，半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为：



    答案：A
    解析：
    提示 根据动量、动量矩、动能的定义，刚体做定轴转动时p=mvc， LO=JOω，T=1/2JOω2。

  • 第2题：

    均质圆盘质量为m，半径为R，在铅垂面绕内O轴转动，图示瞬间角速度为ω，则其对O轴的动量矩大小为（　　）。

    A．mRω
    B．mRω/2
    C．mR2ω/2
    D．3mR2ω/2

    答案：D
    解析：
    根据质点的动量矩公式，体系对O点的动量矩为：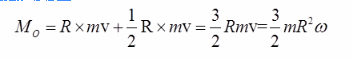

  • 第3题：

    均质圆柱体半径为R，质量为m，绕关于对纸面垂直的固定水平轴自由转动，初瞬时静止（G在O轴的铅垂线上），如图所示。则圆柱体在位置θ=90°时的角速度是（　　）。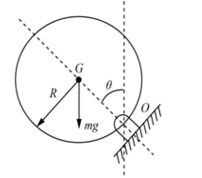



    答案：C
    解析：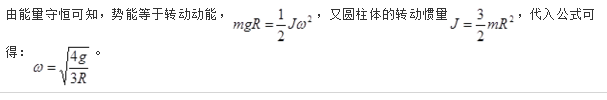

  • 第4题：

    均质圆柱体半径为R，质量为m，绕与纸面垂直的固定水平轴自由转动，初瞬时静止（θ＝0°），如图所示，则圆柱体在任意位置θ时的角速度是（　　）。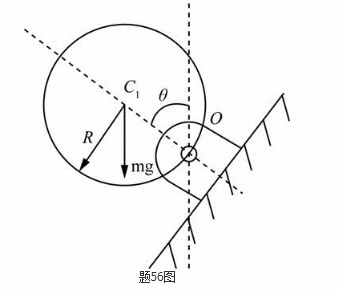



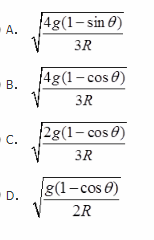    答案：B
    解析：

  • 第5题：

    均质圆环的质量为m半径为R，圆环绕O轴的摆动规律为φ=ωt，ω为常数。图示瞬时圆环对转轴O的动量矩为：


    A. mR2ω
    B. 2mR2ω
    C. 3mR2ω
    D. 1/2mR2ω

    答案：B
    解析：
    提示：定轴转动刚体的动量矩LO= JOω。

  • 第6题：

    轮圈半径为R，其质量M均匀分布在轮缘上，长为R，质量为m的均质辐条固定在轮心和轮缘间，辐条共有2N根。今若将辐条数减少N根，但保持轮对通过轮心、垂直于轮平而轴的转动惯量保持不变，则轮罔的质量应为（）。



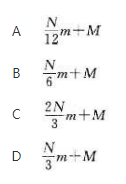    答案：D
    解析：

  • 第7题：

    一个直径100mm重量20kg的圆柱体以轴心线为中心旋转时的转动惯量为多少？假设一个伺服电机经过1：10的减速机后连接到这个圆柱体，那么折算到伺服电机轴上的转动惯量为多少？


    正确答案:圆柱体转动惯量J=1/2*M*R2=1/2*20*25=250kg.cm2
    经过减速比之后折算到电机轴上的转动惯量会减小减速比的平方倍，折算到电机轴上的转动惯量J2=250/100=2.5kg.cm2

  • 第8题：

    两个质量都为100kg的人，站在一质量为200kg、半径为3m的水平转台的直径两端转台的固定竖直转轴通过其中心且垂直于台面初始时，转台每5s转一圈当这两人以相同的快慢走到转台的中心时，转台的角速度ω＝（）（已知转台对转轴的转动惯量J＝MR2/2，计算时忽略转台在转轴处的摩擦）


    正确答案:3.77rad/s

  • 第9题：

    设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）。

    • A、mR2
    • B、mR2/2
    • C、mRω

    正确答案:B

  • 第10题：

    圆柱体定滑轮的质量为m，半径为R，绕其质心轴转动的角位移为θ=a+bt+ct2，a、b、c为常数，作用在定滑轮上的力矩为（）

    • A、（1/2）maR2
    • B、bmR2
    • C、（1/2）mbR2
    • D、mcR2

    正确答案:D

  • 第11题：

    半径为R具有光滑轴的定滑轮边缘绕一细绳，绳的下端挂一质量为m的物体绳的质量可以忽略，绳与定滑轮之间无相对滑动若物体下落的加速度为a，则定滑轮对轴的转动惯量J＝（）。


    正确答案:m（g-a）R2/a

  • 第12题：

    单选题
    质量为2m，半径为R的偏心圆板可绕通过中心O的轴转动，偏心距OC＝ 。在OC连线上的A点固结一质量为m的质点，OA＝R如图示。当板以角速度w绕轴O转动时，系统动量K的大小为（）。（注：C为圆板的质心）。
    A

    K＝0

    B

    K＝mRw

    C

    K＝mRw

    D

    K＝2mRw


    正确答案： C
    解析： 暂无解析

  • 第13题：

    均质圆盘质量为m，半径为R，在铅垂平面内绕O轴转动，图示瞬时角速度为ω，则其对O轴的动量矩和动能大小分别为：



    答案：D
    解析：
    提示 根据定轴转动刚体动量矩和动能的公式LO= JOω, T=1/2JOω2 。

  • 第14题：

    如图所示圆环以角速度ω绕铅直轴AC自由转动，圆环的半径为R，对转轴的转动惯量为I；在圆环中的A点放一质量为m的小球，设由于微小的干扰，小球离开A点。忽略一切摩擦，则当小球达到B点时，圆环的角速度是（　　）。




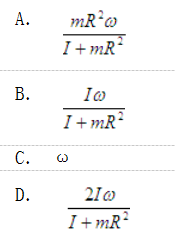    答案：B
    解析：

  • 第15题：

    忽略质量的细杆OC=l，其端部固结匀质圆盘。杆上点C为圆盘圆心。盘质量为m，半径为r。系统以角速度ω绕轴O转动。系统的动能是：


    答案：D
    解析：
    提示 圆盘绕轴O作定轴转动，其动能为T=1/2JOω2。

  • 第16题：

    图4-67示均质圆轮，质量为m,半径为r，在铅垂图面内绕通过圆轮中心O的水平轴以匀角速度ω转动。则系统动量、对中心O的动量矩、动能的大小为（ ）。



    答案：A
    解析：
    提示：根据动量、动量矩、动能的定义，刚体作定轴转动时，ρ = mvc、LO= JOω, T=1/2JOω2。

  • 第17题：

    偏心轮为均质圆盘，其质量为m，半径为R，偏心距OC=R/2。若在图示位置时，轮绕O轴转动的角速度为ω，角加速度为α，则该轮的惯性力系向O点简化的主矢FI和主矩MIO的大小为：



    答案：A
    解析：
    提示：MIO=-JOα，其中 JO = JC + m* OC2 。

  • 第18题：

    设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则此圆柱体的转动惯量为（）。

    • A、mR2
    • B、0.5mR2
    • C、mRω

    正确答案:B

  • 第19题：

    设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）

    • A、mR2；
    • B、mR2/2；
    • C、mRω。

    正确答案:B

  • 第20题：

    已知圆柱体设备半径为r，高为h，密度为γ，则该设备质量公式为（）。

    • A、πrhγ
    • B、πr2hγ
    • C、πr3hγ

    正确答案:B

  • 第21题：

    已知圆柱体设备半径为r，高为h，密度为y，则该设备质量公式为（）。

    • A、πrhy
    • B、πr²hy
    • C、πr³hy

    正确答案:B

  • 第22题：

    一质量为M，半径为R的飞轮绕中心轴以角速度ω作匀速转动，其边缘一质量为m的碎片突然飞出，则此时飞轮的（）。

    • A、角速度减小，角动量不变，转动动能减小
    • B、角速度增加，角动量增加，转动动能减小
    • C、角速度减小，角动量减小，转动动能不变
    • D、角速度不变，角动量减小，转动动能减小

    正确答案:D

  • 第23题：

    均质圆环的质量为m，半径为R，圆环绕O轴的摆动规律为φ=ωt，ω为常数。图4-74所示瞬时圆环对转轴O的动量矩为（）。

    • A、mR2ω
    • B、2mR2ω
    • C、3mR2ω

    正确答案:B

  • 第24题：

    单选题
    设质量分布均匀的圆柱体的质量为m，半径为R，绕中心旋转时的角速度为ω，则圆柱体的转动惯量为（）
    A

    mR2；

    B

    mR2/2；

    C

    mRω。


    正确答案： C
    解析： 暂无解析

相关内容