假设某损失分布服从二项分布,损失概率P=0.002,风险单位的数量为N。当N=1000时,期望损失为( )。假设某损失分布服从二项分布，损失概率P=0.002，风险单位的数量为N。1.当N=1000时，期望损失为( )。A.0.02B.2C.1000D.条件不足，无法计算

题目
假设某损失分布服从二项分布,损失概率P=0.002,风险单位的数量为N。当N=1000时,期望损失为( )。

假设某损失分布服从二项分布，损失概率P=0.002，风险单位的数量为N。

1.当N=1000时，期望损失为( )。

A.0.02

B.2

C.1000

D.条件不足，无法计算

相似考题

1.假设汽车损失额及概率分布如下表所示：1.前述汽车损失分布的期望值为( )。A.5000B.21300C.2600D.10002.前述汽车损失分布的标准差为( )。A.13978B.1000C.2600D.1000003.前述汽车损失分布的变异系数为( )。A.10.32B.5.38C.75150D.10004.假设某汽车运输公司共有相同的车辆100台，每台汽车都独立地服从上表所示的损失概率分布，则该汽车运输公司汽车损失总额的标准差为( )。A.260000B.26000C.10000D.1397805.假设其他条件不变，汽车运输公司的车辆从100台变成1000台，那么该公司汽车损失的变异系数变为原来的( )倍。A.10B.1/10C.√10D.1/√10

2.第2－4题为套题：假设某损失分布服从二项分布，损失概率P＝0.002，风险单位的数量为N。当N＝1000时，期望损失为()。A.0.02B.2C.1000D.条件不足，无法计算

3.在某事件的每次实验中，设成功的概率为P，则失败的概率为Q（＝1-P），在n次实验中，该事件成功k次的概率为Pn（k）＝CnkPk（1-P）n-k，问成功次数k服从什么分布A、泊松分布B、二项分布C、正态分布D、F分布E、超儿何分布

4.已知随机变量X服从二项分布,且E(X)=2.4,D(X)=1.44,则二项分布的参数n,p的值为()。A、n=4，p=0.6B、n=6，p=0.4C、n=4，p=0.3D、n=24，p=0.1

更多“假设某损失分布服从二项分布,损失概率P=0.002,风险单位的数量为N。当N=1000时,期望损失为( )。 ”相关问题

  • 第1题：

    通过风险估测,我们希望得到哪些信息()。

    A、每一风险所引起的致损事故发生的概率和损失分布

    B、单一风险单位的损失程度

    C、几种风险对同一单位所致损失的概率和损失分布

    D、所有风险单位损失的期望值和方差


    答案：ABCD

  • 第2题：

    对于X服从二项分布B(n,p),则E(X)=p。()


    正确答案:错

  • 第3题：

    损失概率计算包括（ ）。

    A．某一风险在足够长的时间内发生损失的次数

    B．一个风险单位同时遭受多种风险事故所致单一损失情况下的损失概率计算

    C．一个风险单位不同时遭受多种风险事故所致单一损失情况下的损失概率计算

    D．N个独立的风险单位遭受同一风险事故所致损失的损失概率计算


    参考答案：BCD

  • 第4题：

    第 52－54 题为套题： 假设某损失分布服从二项分布，损失概率P＝002，风险单位的数量为N。 52．当N＝1000 时，期望损失为( )。

    A.0．02

    B.2

    C.1000

    D.条件不足，无法计算


    参考答案：B
    P116，倒12－5行

  • 第5题：

    已知随机变量X服从二项分布，且E(X)=2.4，D(X)=1.44，则二项分布的参数n,p分别是：

    A. n=4,p=0. 6
    B. n=6,p=0.4
    C. n=8,p=0.3
    D.n=24,p=0. 1

    答案：B
    解析：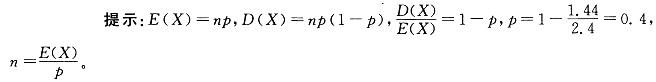

  • 第6题：

    若X服从二项分布b（k；n，p），则EX=npq


    正确答案:错误

  • 第7题：

    已知随机变量X服从二项分布，且EX=2.4，DX=1.44，则二项分布的参数n，p的值为（）。

    • A、n=4，p=0.6
    • B、n=6，p=0.4
    • C、n=8，p=0.3
    • D、n=24，p=0.1

    正确答案:B

  • 第8题：

    若随机变量X服从参数为n和p的二项分布，则它的数学期望为（），方差是（）


    正确答案:np；npq

  • 第9题：

    损失严重程度的决定因素是（）。

    • A、损失概率分布、损失期望值和损失程度
    • B、损失概率分布、损失期望值和损失范围
    • C、损失概率分布、损失范围和损失程度
    • D、损失范围、损失期望值和损失程度

    正确答案:A

  • 第10题：

    多选题
    下列有关风险汇聚的效果的说法中，错误的有（）。
    A

    当风险是相互独立的时候，汇聚安排可以抑制风险

    B

    风险汇聚能够改变每个人的期望损失

    C

    风险汇聚能够降低平均损失的标准差

    D

    当风险汇聚的加入者增加时，出现极端损失的概率不断降低

    E

    随着加入者数量的增加，每个人承担的平均损失的概率分布逐渐接近于U形曲线


    正确答案： D,B
    解析： B项，风险汇聚不能改变每个人的期望损失，但能将平均损失的标准差减小，使事故损失变得更容易预测，因此风险汇聚降低了每个人的风险；E项，随着加入者数量的增加，每个人承担的平均损失的概率分布逐渐接近于钟形曲线。

  • 第11题：

    单选题
    损失严重程度的决定因素是（）。
    A

    损失概率分布、损失期望值和损失程度

    B

    损失概率分布、损失期望值和损失范围

    C

    损失概率分布、损失范围和损失程度

    D

    损失范围、损失期望值和损失程度


    正确答案： A
    解析： 暂无解析

  • 第12题：

    单选题
    二项分布B（n，p）的数学期望为（）
    A

    n（1-n）p

    B

    np（1-p）

    C

    np

    D

    n（1-p）


    正确答案： C
    解析： 暂无解析

  • 第13题：

    单个债务的信用风险预期损失( )。

    A．预期损失等于违约概率乘以违约风险暴露

    B．预期损失等于违约概率乘以违约损失率乘以违约风险暴露

    C．预期损失可以估计

    D．预期损失是未来损失的最大值

    E．预期损失是信用风险损失分布的数学期望


    正确答案：BCE

  • 第14题：

    风险衡量所提供的主要信息有（ ）。

    A．每一风险所引起的致损事故发生的概率和损失分布

    B．几种风险对同一单位所致损失的概率和损失分布

    C．单一风险单位的损失幅度，并在此基础上，进一步估测整个企业发生致损事故的概率和总损失分布，以及某一时期内的总损失金额

    D．所有风险单位损失的期望值和标准差


    参考答案：ABCD

  • 第15题：

    损失严重程度的决定因素是（ ）。

    A.损失概率分布、损失期望值和损失程度

    B.损失概率分布、损失期望值和损失范围

    C.损失概率分布、损失范围和损失程度

    D.损失范围、损失期望值和损失程度


    参考答案：A

  • 第16题：

    已知随机变量X服从二项分布，且E(X)=2.4，D(X)=1.44，则二项分布的参数n、p分别为( )。

    A.n=4，p=06
    B.n=24，p=144
    C.n=6，p=04
    D.n=6，p=06

    答案：C
    解析：
    E(X)=np，D(X)=np(1-p)

  • 第17题：

    有关二项分布正确的是（）

    • A、二项分布的变量是连续型变量
    • B、Excel中NORMDIST（）函数计算二项分布的概率
    • C、二项分布由n和p两个参数决定
    • D、二项分布中平均值为μ=n/p

    正确答案:C

  • 第18题：

    设随机变量X服从以n，p为参数的二项分布，且EX=15，DX=10，则n=（）。


    正确答案:45

  • 第19题：

    设X服从二项分布，EX=2.4，DX=1.44，则二项分布的参数为（）.

    • A、n=6，p=0.4
    • B、n=6，p=0.1
    • C、n=8，p=0.3
    • D、n=24，p=0.1

    正确答案:A

  • 第20题：

    二项分布B（n，p）的数学期望为（）

    • A、n（1-n）p
    • B、np（1-p）
    • C、np
    • D、n（1-p）

    正确答案:C

  • 第21题：

    单选题
    若某人群某疾病发生的阳性数X服从二项分布，则从该人群中随机抽出n个人，阳性数X不少于k人的概率为（）。
    A

    P（k+1）+P（k+2）+…+P（n）

    B

    P（0）+P（1）+…+P（k）

    C

    P（0）+P（1）+…+P（k+1）

    D

    P（k）+P（k+1）+…+P（n）

    E

    P（1）+P（2）+…+P（k）


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    设某险种的实际损失额有几种可能：25、50、75、100、200、500，发生的概率分别为0.2、0.3、0.2、0.15、0.1、0.05，假设损失次数服从参数为r=10、β=0.3的奇异负二项分布，免赔额为50，则理赔次数的分布为（　　）。
    A

    NB（10，0.3）

    B

    NB（10，0.15）

    C

    B（10，0.3）

    D

    B（10，0.15）

    E

    B（10，0.45）


    正确答案： C
    解析：
    X表示索赔额，则索赔的概率为：
    υ=P（X＞50）=0.2+0.15+0.1+0.05=0.5
    以N*表示免赔额为50时的理赔次数，则其概率母函数为：
    PN*（t）={1-0.3[1+0.5（t-1）-1]}-10=[1-0.15（t-1）]-10
    所以理赔次数服从奇异二项分布，参数分别为10和0.15。

  • 第23题：

    多选题
    下列关于几种概率分布之间的关系的陈述中，正确的有（）。
    A

    二点分布（0－1分布）是二项分布的特例

    B

    当n很大而p又很小时，二项分布可用参数λ＝np的泊松分布近似

    C

    当N很大而M/N很小是，超几何分布趋于二项分布

    D

    当n＞30时，不管p大小，二项分布的概率都可用正态分布来近似计算

    E

    当n无限增大时，二项分布趋近于正态分布


    正确答案： D,A
    解析： 暂无解析

相关内容