火的三要素是燃烧的（ ）。A．必要条件B．充分条件C．必要且充分条件D．充要条件
题目
火的三要素是燃烧的（ ）。
A．必要条件
B．充分条件
C．必要且充分条件
D．充要条件
相似考题
更多“火的三要素是燃烧的（ ）。A．必要条件B．充分条件C．必要且充分条件D．充要条件”相关问题
-
第1题：
将充分条件和必要条件合并,即成为充分必要条件,简称()。A.充分条件
B.要充条件
C.必要条件
D.充要条件
参考答案：D
-
第2题：
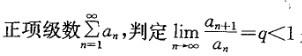是此正项级数收敛的什么条件？
A.充分条件，但非必要条件 B.必要条件，但非充分条件
C.充分必要条件 D.既非充分条件，又非必要条件答案：A解析：提示:利用正项级数比值法确定级数收敛，而判定正项级数收敛还有其他的方法，因而选A。 -
第3题：
函数z=f(x，y)在点(x，y)处的偏导数存在是函数在该点可微的()A.必要条件
B.充分条件
C.既非必要又非充分条件
D.充要条件答案：A解析：因为对于二元函数而言，在某点的偏导数存在，未必推出在该点可微，但是二元函数在某点可微，则在该点的偏导数一定存在，故应选A答案． -
第4题：
正项级数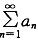
收敛是级数
收敛的什么条件？
A.充分条件，但非必要条件
B.必要条件，但非充分条件
C.充分必要条件
D.既非充分条件，又非必要条件答案：A解析：提示：利用正项级数比较判别法--极限形式判定，反之不一定正确。 -
第5题：
设甲：a＞0且b＞0；乙：ab＞0，则甲是乙的（ ）A.充分条件，但非必要条件
B.必要条件，但非充分条件
C.既非充分条件，也非必要条件
D.充分必要条件答案：A解析：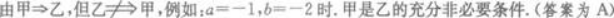
-
第6题：
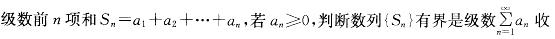敛的什么条件？
A.充分条件，但非必要条件
B.必要条件，但非充分条件
C.充分必要条件
D.既非充分条件，又非必要条件答案：C解析：提示 用正项级数基本定理判定。 -
第7题：
零为矩阵A的特征值是A为不可逆的A.充分条件
B.必要条件
C.充要条件
D.非充分、非必要条件答案：C解析： -
第8题：
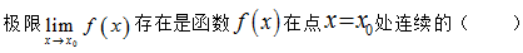A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件答案：B解析：
-
第9题：
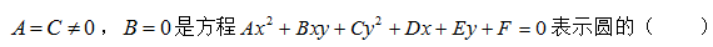A.充分不必要条件
B.必要不充分条件
C.充要条件
D.不充分不必要条件答案：A解析：
-
第10题：
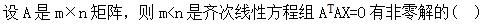A.必要条件
B.充分条件
C.充要条件
D.以上都不对答案：B解析：
-
第11题：
火的三要素是燃烧的（）。
- A、必要条件
- B、充分条件
- C、必要且充分条件
- D、充要条件
正确答案:A -
第12题：
单选题火的三要素是燃烧的（）。A必要条件
B充分条件
C必要且充分条件
D充要条件
正确答案： B解析： 暂无解析 -
第13题：
A.必要条件
B.充分条件
C.充要条件
D.以上均不对答案：B解析：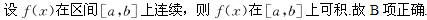
-
第14题：
正项级数
收敛的什么条件？
A.充分条件，但非必要条件 B.必要条件，但非充分条件
C.充分必要条件 D.既非充分条件，又非必要条件答案：A解析：提示:利用正项级数比较判别法--极限形式判定，反之不一定正确。 -
第15题：
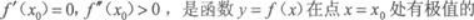A.必要条件
B.充要条件
C.充分条件
D.无关条件答案：C解析：根据极值充分条件定理选c． -
第16题：
设条件甲为：0A.乙是甲的充分条件，但不是甲的必要条件．
B.乙是甲的必要条件，但不是甲的充分条件．
C.乙是甲的充要条件．
D.乙不是甲的充分条件，也不是甲的必要条件．答案：B解析：第17题：
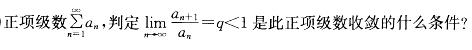A.充分条件，但非必要条件
B.必要条件，但非充分条件
C.充分必要条件
D.既非充分条件，又非必要条件答案：A解析：提示 利用正项级数比值法确定级数收敛，而判定正项级数收敛还有其他的方法，因而选A。第18题：
A.充分条件而非必要条件
B.必要条件而非充分条件
C.充分必要条件
D.既非充分条件又非必要条件答案：D解析：多元函数的偏导数存在性与连续没有关系。第19题：
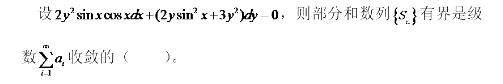A.充分必要条件
B.充分非必要条件
C.必要非充分条件，
D.非充分且非必要条件答案：A解析：第20题：
A.充分而不必要条件
B.必要而不充分条件
C.充要条件
D.既不充分又不必要条件答案：C解析：
第21题：
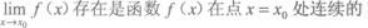A.充分非必要条件
B.必要非充分条件
C.充分必要条件
D.既非充分条件也非必要条件答案：B解析：由连续与极限的关系知选B．第22题：
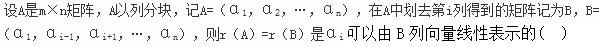A.充分条件
B.必要条件
C.充要条件
D.既不充分又不必要条件答案：C解析：
第23题：
单选题已知p是r的充分条件而不是必要条件，q是r的充分条件，s是r的必要条件，q是s的必要条件，现有下列命题：①s是q的充要条件；②p是q的充分条件而不是必要条件；③r是q的必要条件而不是充分条件；④﹁p是﹁s的必要条件而不是充分条件；⑤r是s的充分条件而不是必要条件。则正确命题的序号是（ ）。A①④⑤
B①②④
C②③⑤
D②④⑤
正确答案： D解析：
由“q是r的充分条件”和“s是r的必要条件”可以得到“q是S的充分条件”，又由于“q是s的必要条件”可知“s是q的充要条件”，①成立；由“p是r的充分条件”和“s是r的必要条件”可以得到“p是s的充分条件”，又由“q是s的必要条件”可以得到“p是q的充分条件”，但得不到“p是q的必要条件”，所以②成立；由“q是r的充分条件”、“s是r的必要条件”和“q是s的必要条件”可以得到“r是q的充要条件”，③不成立；因为“p是s的充分条件但不是必要条件”是真命题，那么逆否命题也是真命题，即“﹁p是﹁s的必要条件而不是充分条件”正确，④成立；由“q是r的充分条件”、“s是r的必要条件”和“q是s的必要条件”可以得到“r是s的充要条件”，⑤不成立。